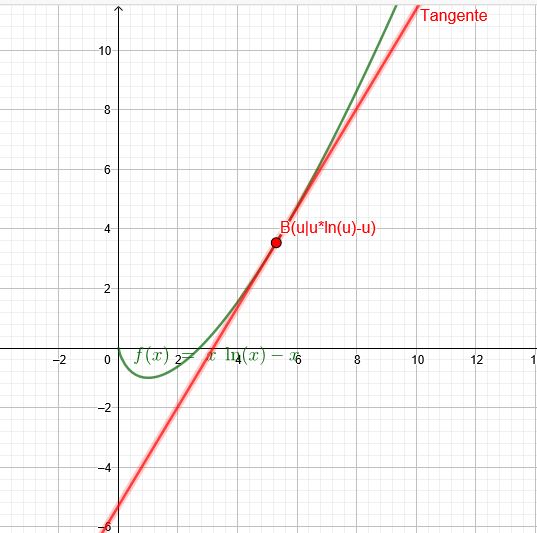
\(f_a(x)=x•ln(x)-a• x\) Mit \(a=1\):
\(f_1(x)=x•ln(x)- x\)
\(f'_1(x)=ln(x)+x•\frac{1}{x}- 1\)
\(f'_1(x)=ln(x)\)
\(f_1(u)=u•ln(u)- u\)
\(f'_1(u)=ln(u)\)
Tangentengleichung:
\(\frac{y-(u•ln(u)- u)}{x-u}=ln(u)\)
Nullstelle: \(y=0\)
\(\frac{0-(u•ln(u)- u)}{x-u}=ln(u)\)
\(-(u•ln(u)- u)=ln(u)•(x-u)\)
\(-u•ln(u)+u=ln(u)•x-ln(u)•u\)
\(u=ln(u)•x\)
\(x=\frac{u}{ln(u)}\)
Schnitt mit der y-Achse: \(x=0\)
\(\frac{y-(u•ln(u)- u)}{0-u}=ln(u)\)
\(\frac{y+(u•ln(u)- u)}{u}=ln(u)\)
\(y+(u•ln(u)- u)=ln(u)•u\)
\(y-(-u•ln(u)+ u)=ln(u)•u\)
\(y=ln(u)•u+(-u•ln(u)+ u)\)
\(y=ln(u)•u-u•ln(u)+ u\)
\(y= u\)
Dreiecksfläche:
\(A(u)= \frac{1}{2}•u•\frac{u}{ln(u)} \)
\(A(u)= \frac{u^2}{2•ln(u)} \)
\(A'(u)=\frac{2u•2 ln(u)-u^2•\frac{2}{u}}{4•ln^{2}(u)} \)
\(A'(u)=\frac{4u• ln(u)-2u}{4•ln^{2}(u)} \)
\(\frac{4u• ln(u)-2u}{4•ln^{2}(u)}=0 \)
\(2u• ln(u)=u \)
\(2u• ln(u)-u=0 \)
\(u•(2• ln(u)-1)=0 \)
\(u_1=0\)
\(2• ln(u)=1 \)
\(ln(u)=\frac{1}{2} \)
\( e^{ln(u)}=e^{\frac{1}{2}} \)
\( u= e^{\frac{1}{2}} \)
\(A(e^{\frac{1}{2}})= \frac{1}{2}•e^{\frac{1}{2}}•\frac{e^{\frac{1}{2}}}{ln(e^{\frac{1}{2}})} \) mit \(\ln(e)=1\)
\(A= 0,25•e\)