Aufgabe:Textaufgabe zur Analytische Geometrie

Text erkannt:
Aufgabe:
Ein U-Boot macht sich mit mehreren Hobby-Tauchern an Bord auf den Weg, um die blauschwarzen Tiefen des Meeres zu erkunden. Die Tauchkreuzfahrt bietet die Möglichkeit, skurrile Tiefseebewohner zu beobachten. So sind auch schlafende Tiefseehaie keine Seltenheit.
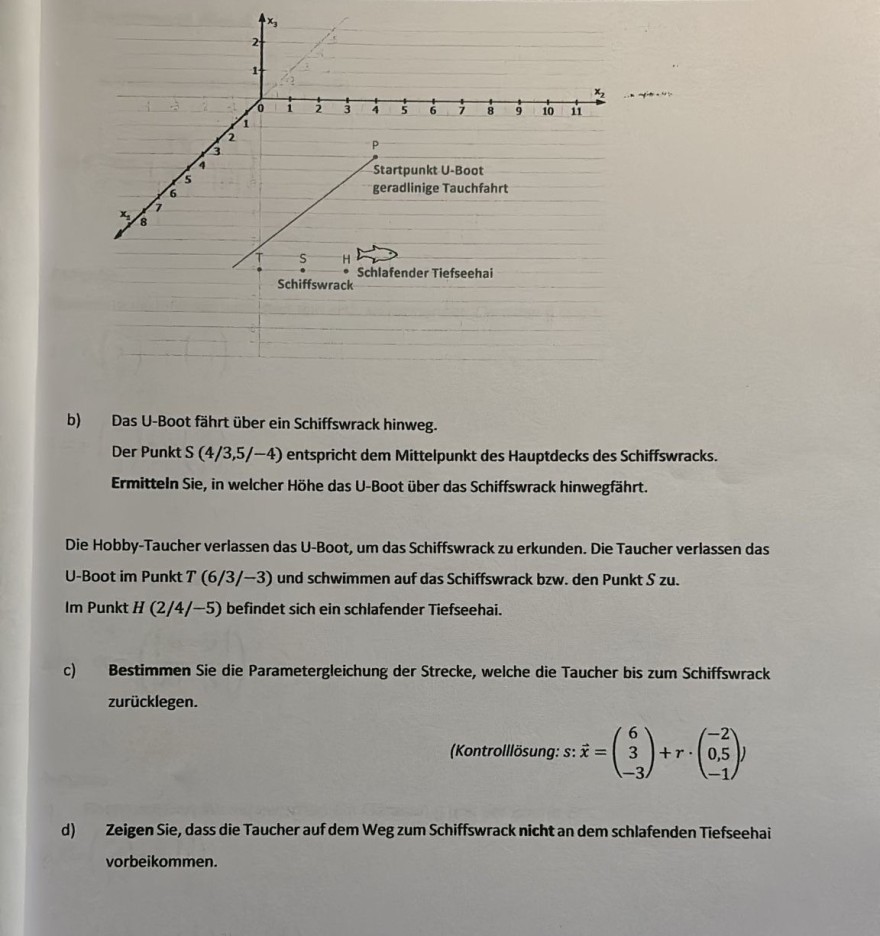
Das U-Boot begibt sich kurz nach dem Beginn seiner Tauchfahrt im Punkt \( P(2 / 5 /-1) \) in eine geradlinige Bahn, wobei sein in einer Minute zurückgelegter Weg dem Vektor \( \vec{v}=\left(\begin{array}{c}4 \\ -3 \\ -2\end{array}\right) \) entspricht (vgl. Abbildung auf der nächsten Seite).
Hinweise:
1 Längeneinheit entspricht \( 1 m, x_{3} \) gibt die Höhe des U-Bootes unter der Wasseroberfläche an. Die Wasseroberfläche wird durch die \( x_{1} x_{2} \)-Ebene beschrieben. Die Zeit \( t \) wird in Minuten angegeben.
a) Nach 8 Minuten erreicht das U-Boot den Rand eines Korallenriffs.
Ermitteln Sie, wie viele Meter sich das U-Boot zu diesem Zeitpunkt unter der Wasseroberfläche befindet.
Text erkannt:
b) Das U-Boot fährt über ein Schiffswrack hinweg.
Der Punkt S \( (4 / 3,5 /-4) \) entspricht dem Mittelpunkt des Hauptdecks des Schiffswracks.
Ermitteln Sie, in welcher Höhe das U-Boot über das Schiffswrack hinwegfährt.
Die Hobby-Taucher verlassen das U-Boot, um das Schiffswrack zu erkunden. Die Taucher verlassen das U-Boot im Punkt \( T(6 / 3 /-3) \) und schwimmen auf das Schiffswrack bzw. den Punkt \( S \) zu. Im Punkt \( H(2 / 4 /-5) \) befindet sich ein schlafender Tiefseehai.
c) Bestimmen Sie die Parametergleichung der Strecke, welche die Taucher bis zum Schiffswrack zurücklegen.
\( \text { (Kontrolllösung: } s: \vec{x}=\left(\begin{array}{c} 6 \\ 3 \\ -3 \end{array}\right)+r \cdot\left(\begin{array}{c} -2 \\ 0,5 \\ -1 \end{array}\right) \text { ), } \)
d) Zeigen Sie, dass die Taucher auf dem Weg zum Schiffswrack nicht an dem schlafenden Tiefseehai vorbeikommen.

Text erkannt:
Winkel zwischen zwei Geraden
\( \cos \propto=\left(\frac{|\vec{u} \cdot \vec{v}|}{|\vec{u}| \cdot|\vec{v}|}\right) \)
Aufgabe
Bestimme den Winkel zwischen den sich schneidenden Geraden \( \mathrm{g} \) und \( \mathrm{h} \) :
\( g: \vec{x}=\left(\begin{array}{c} -7 \\ 1 \\ 0 \end{array}\right)+r \cdot\left(\begin{array}{c} 5 \\ -1 \\ 2 \end{array}\right) \)
\( h: \vec{x}=\left(\begin{array}{c}3 \\ -1 \\ 4\end{array}\right)+s \cdot\left(\begin{array}{c}-3 \\ -2 \\ 1\end{array}\right) \)
Winkel zwischen Gerade und Ebene
\( \sin \propto=\left(\frac{|\stackrel{\rightharpoonup}{n} \cdot \stackrel{\rightharpoonup}{v}|}{|\stackrel{\rightharpoonup}{n}| \cdot|\stackrel{\rightharpoonup}{v}|}\right) \)
Aufgabe
a) Bestimme den Winkel zwischen der Geraden g und der Ebene \( \mathrm{E} \) :
\( \begin{array}{l} g: \vec{x}=\left(\begin{array}{c} 3 \\ -8 \\ 7 \end{array}\right)+r \cdot\left(\begin{array}{c} 5 \\ 0 \\ 2 \end{array}\right) \\ E: \vec{x}=\left(\begin{array}{c} 2 \\ -1 \\ 4 \end{array}\right)+s \cdot\left(\begin{array}{c} 1 \\ -7 \\ 3 \end{array}\right)+u \cdot\left(\begin{array}{c} 2 \\ 2 \\ -1 \end{array}\right) \end{array} \)
b) Bestimme den Winkel zwischen der Geraden g (vgl. Aufgabe a) und der \( x_{1} x_{2} \)-Ebene.
Ich schreibe morgen eine Klausur zur Analytische Geometrie. Meine Lehrerin hat die folgende Probearbeit zum üben hochgeladen. Kann mir jemand helfen die Aufgaben zu lösen? Das habe ich bis jetzt:
Problem/Ansatz:
Aufgabe 1)
a)
Ich habe einfach den Vektor V mal 8 plus den Punkt P gerechnet und davon X3 als Tiefe/Höhe benutzt. Weil Punkt P die Startposition ist und dann plus den Vektor mal 8, weil der Vektor ja beschreibt wie er sich in einer Minute bewegt. Also, habe ich 17m nach 8min raus.
Zu den restlichen Aufgaben habe ich keinen Plan wie ich die lösen würde. Außer vielleicht die mit den Winkeln. Obwohl mich da die b) Aufgabe verwirrt.