Aufgabe:
Der sehr hohe Raum in Fig. 1 wurde
durch das dreieckige Segeltuch, das an den
Stellen A, B und C befestigt wurde, wohnlicher
gestaltet. Das Tuch ist so gespannt, dass seine
Oberfläche als Ausschnitt einer Ebene angesehen werden kann. Geben Sie eine Parametergleichung der Ebene E an, die durch die
Befestigungspunkte des Segeltuches festgelegt wird. Legen Sie hierzu ein geeignetes
Koordinatensystem fest.
Problem/Ansatz:
Ich hatte die Aufgabe soweit ausgerechnet. Vergleichsergebnis aus der Unterrichtsstunde bzw. eine mögliche Parametergleichung für die Ebene war: E:x= (0/4/4,5)+r*(4/-4/-1)+s*(0/2/-2). Ist meine Lösung aus dem Bild ebenfalls richtig?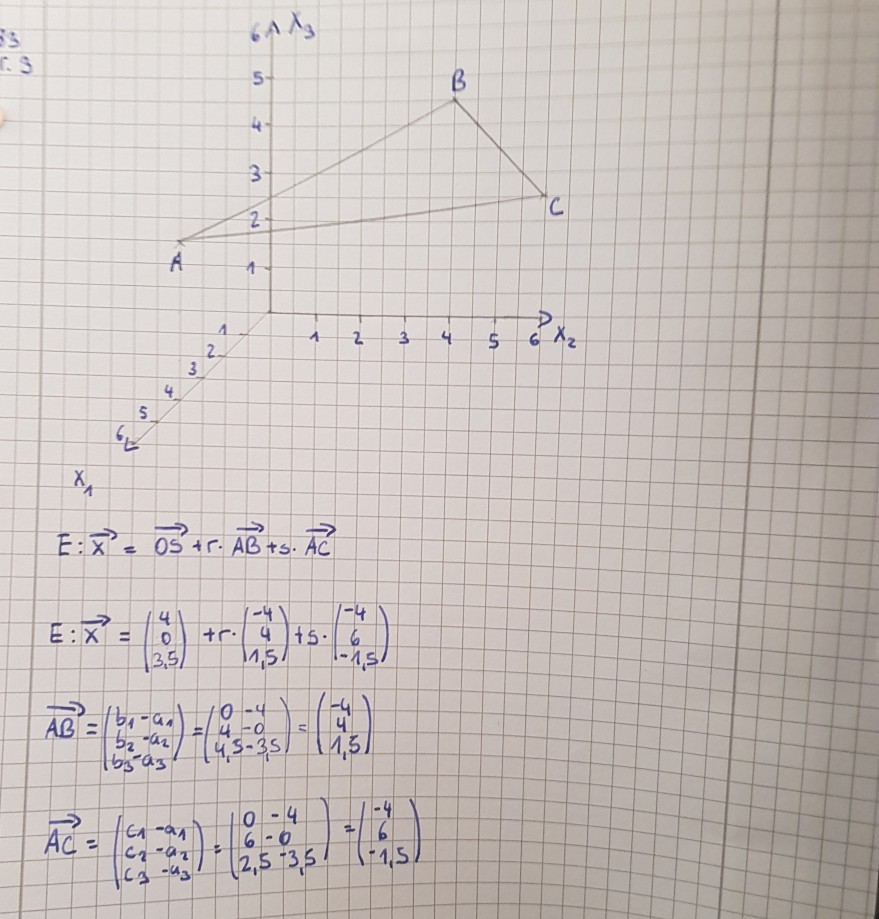
Text erkannt:
\( 6 \hat{}_{3} X_{3} \)
B
\( x_{1} \)
\( E: \vec{x}=\overrightarrow{O S}+r \cdot \overrightarrow{A B}+s \cdot \overrightarrow{A C} \)
\( E: \vec{x}=\left(\begin{array}{l}4 \\ 0 \\ 3,5\end{array}\right)+r \cdot\left(\begin{array}{c}-4 \\ 4 \\ 1,5\end{array}\right)+5 \cdot\left(\begin{array}{c}-4 \\ 6 \\ -1,5\end{array}\right) \)
\( \overrightarrow{A B}=\left(\begin{array}{l}b_{1}-a_{1} \\ b_{2}-a_{2} \\ b_{3}-a_{3}\end{array}\right)=\left(\begin{array}{cc}0 & -4 \\ 4 & -0 \\ 4_{1} & 5-3,5\end{array}\right)=\left(\begin{array}{c}-4 \\ 4 \\ 1,5\end{array}\right) \)
\( \overrightarrow{A C}=\left(\begin{array}{ll}c_{1} & -a_{1} \\ c_{2} & -a_{2} \\ c_{3} & -u_{3}\end{array}\right)=\left(\begin{array}{ll}0 & -4 \\ 6 & -0 \\ 2,5 & -3,5\end{array}\right)=\left(\begin{array}{c}-4 \\ 6 \\ -1,5\end{array}\right) \)