Zunächst das Baumdiagramm:
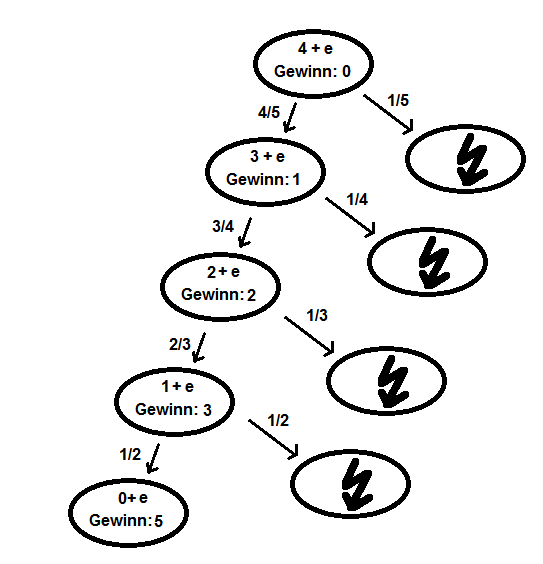
In den Knoten ist jeweils angegeben, Wieviele Bonbons noch da sind, dabei wird zwischen normalen Bonbons und dem elektrischen Bonbon unterscheiden. Außerdem ist angegeben, wieviele Bonbons Mirka bereits gewonnen hat.
An den Kanten ist die Wahrscheinlichkeit angegeben, mit der man zum Folgeknoten gelangt.
Um die Wahrscheinlichkeit zu berechnen, einen bestimmten Knoten zu erreichen, multipliziert man die Wahrscheinlichkeiten, die auf dem Pfad zu diesem Knoten angegeben sind, miteinander.
Also:
a)
Die Wahrscheinlichkeit, dass Mirka alle Bonbons gewinnt, beträgt:
( 4 / 5 ) * ( 3 / 4 ) * ( 2 / 3 ) * ( 1 / 2 ) = 1 / 5 = 0,2 = 20 %
b)
Die Wahrscheinlichkeit, dass Mirka zwei Bonbons gewinnt, beträgt:
( 4 / 5 ) * ( 3 / 4 ) = 3 / 5 = 0,6 = 60 %
Die Wahrscheinlichkeit, dass Mirka drei Bonbons gewinnt, beträgt:
( 4 / 5 ) * ( 3 / 4 ) * ( 2 / 3 ) = 2 / 5 = 0,4 = 40 %