Aufgabe:
Ein Ballon startet im Punkt A(2/5/0). Er bewegt sich geradlinig mit konstanter Geschwindigkeit und ist nach 1 Stunde im Punkt B(4/8/1). Beim Start des Ballons befindet sich ein Flugzeug im Punkt C(10/15/1) und fliegt mit 90 km/h in Richtung u⃗ = (-1 -2 2) (alle Koordinaten in km).
a) Wie weit ist der Punkt C vom Startplatz A des Ballons entfernt?
habe ich gelöst, ist einfach.
Meine Lösung ist 12,8452 km.
b) Wie viele Minuten nach dem Start des Ballons kommen sich der Ballon und das Kleinflugzeug am nächsten? Wie weit sind sie in diesem Augenblick voneinander entfernt?
Mein Lösungsansatz habe ich unten:
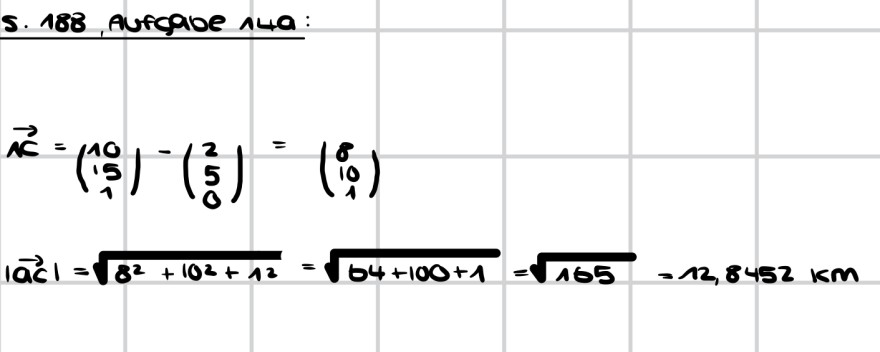
Text erkannt:
5. 188 , Aufcabe 14a:
\( \begin{array}{l} \overrightarrow{A C}=\left(\begin{array}{c} 10 \\ 15 \\ 1 \end{array}\right)-\left(\begin{array}{l} 2 \\ 5 \\ 0 \end{array}\right)=\left(\begin{array}{l} 8 \\ 0 \\ 1 \end{array}\right) \\ |\overrightarrow{a C}|=\sqrt{8^{2}+10^{2}+12}=\sqrt{64+100+1}=\sqrt{165}=12,8452 \mathrm{~km} \end{array} \)

Text erkannt:
Avfgabe 140:
\( \begin{array}{l} \vec{u}=\overrightarrow{A B}=\left(\begin{array}{l} 4 \\ 0 \\ 1 \end{array}\right)-\left(\begin{array}{l} 2 \\ 5 \\ 0 \end{array}\right)=\left(\begin{array}{l} 2 \\ 3 \\ 1 \end{array}\right) \\ B: \vec{x}=\left(\begin{array}{l} 2 \\ 5 \\ 0 \end{array}\right)+t \cdot\left(\begin{array}{l} 2 \\ 3 \\ 1 \end{array}\right) \end{array} \)
\( \begin{array}{l} F: \vec{x}=\left(\begin{array}{c} 10 \\ 15 \\ 1 \end{array}\right)+S \cdot\left(\begin{array}{c} -30 \\ -60 \\ 60 \end{array}\right) \\ \left(\begin{array}{l} 2 \\ 3 \\ 1 \end{array}\right)=k \cdot\left(\begin{array}{c} -30 \\ -60 \\ 60 \end{array}\right) \end{array} \)
I. \( 2=-30 \mathrm{k} \quad(:(-30) \)
\( k=-\frac{1}{15} \)
II. \( 3=-60 k \quad 1:(-6) \quad k=-\frac{1}{20} \)
III. \( A=60 \mathrm{~K} 1: 60 \)
\( k=\frac{1}{60} \)
nicht collinear

Text erkannt:
\( \begin{array}{l} \left(\begin{array}{l} 2 \\ 5 \\ 0 \end{array}\right)^{+t} \cdot\left(\begin{array}{l} 2 \\ 3 \\ 1 \end{array}\right)=\left(\begin{array}{l} 10 \\ 15 \\ 1 \end{array}\right)+5 \cdot\left(\begin{array}{c} -30 \\ -60 \\ 60 \end{array}\right) \\ \text { I. } 2+2 t=10-30 \text { s } 1-210 \\ 2 t=8-3051+305 \\ 2 t+30 s=8 \\ 5+3 t=10-605 \quad 1-5 \\ 3 t=10-6051+605 \\ 3 t+60 s=10 \\ \end{array} \)
II.
\( \begin{array}{l} 5+3 t=16-605 \quad 1-5 \\ 3 t=10-6051+605 \\ 3 t+60 s=10 \end{array} \)
III \( t=1+6051-605 \)
\( t-60 s=1 \)
Nachdem ich die Gleichungen der Gleichungssystem aufgestellt habe weiß ich nun nicht, was ich machen soll. Kann mir jemand helfen?