Aufgabe:
Filmkulisse
In einer Filmkulisse ist ein Haus aufge-baut, dessen Dach eine quadratische Pyramide mit den Grundflächenecken A (6|4|2), B (6|6|2), C(4|6|2), D (4|4|2) und der Spitze S ist. Die Dachpyramide ist 2m hoch. Ein Scheinwerfer bei L(5|1012) beleuchtet das Haus von rechts. In der x-2-Ebene ist eine Leinwand aufgespannt, auf der ein Schatten des Hauses entsteht.
a) Wie lauten die Koordinaten der Pyramidenspitze S?
b) Berechnen Sie das Volumen V und die sichtbare Oberfläche O der Dachpyramide.
c) Welchen Winkel bilden die Dachbalken AS und BS bei S?
d) Berechnen Sie das Schattenbild S' der Pyramidenspitze S auf der Leinwand.
Die Eckpunkte B und C haben die Schattenpunkte B'(7,5|0|2) und C' (2,5|0|2). Zeigen Sie:
Das Schattendreieck B'C'S' ist ein gleichschenkliges Dreieck.
e) Zeigen Sie, dass der Vektor v senkrecht auf der Dachfläche BCS steht.
v=(0|-2|-1)
f) Ein Lichtstrahl in Richtung des Vektors V erzeugt einen Schattenpunkt der Pyramidenspit-ze S. Liegt dieser Schattenpunkt auf der Bodenebene oder auf der Leinwand?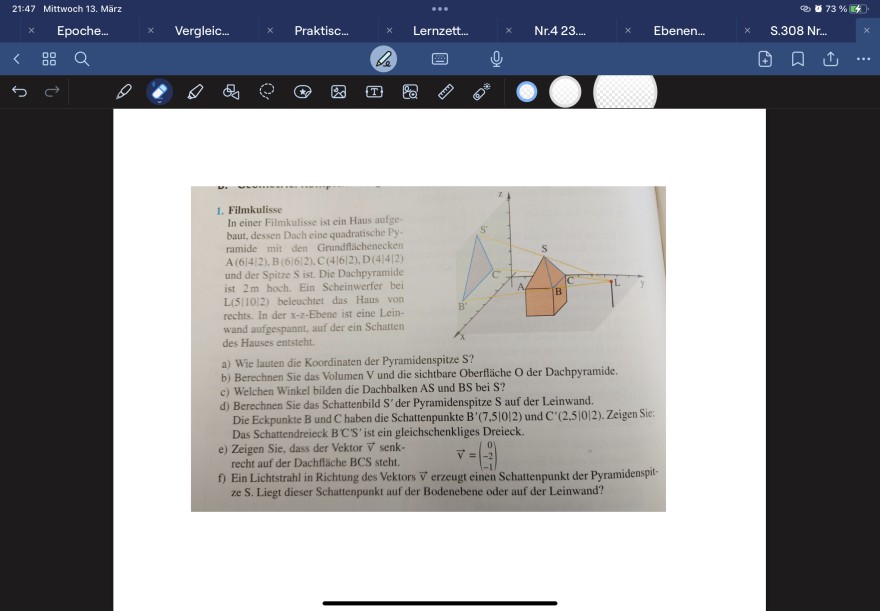
Text erkannt:
1. Filmkulisse
In einer Filmkulisse ist ein Haus aufgebaut, dessen Dach eine quadratische Pyramide mit den Grundflächenecken \( \mathrm{A}(6|4| 2), \mathrm{B}(6|6| 2), \mathrm{C}(4|6| 2), \mathrm{D}(4|4| 2) \) und der Spitze \( S \) ist. Die Dachpyramide ist \( 2 \mathrm{~m} \) hoch. Ein Scheinwerfer bei U(5)i0|2) beieuchtel das Haus von. rechts. In der \( x-z \)-Ebene ist eine Leinwand aufgespannt, auf der ein Schatten des Hauses entsteht.
a) Wie lauten die Koordinaten der Pyramidenspitze S?
b) Berechnen Sie das Volumen V und die sichtbare Oberfläche O der Dachpyramide.
c) Welchen Winkel bilden die Dachbalken AS und BS bei S?
d) Berechnen Sie das Schattenbild S' der Pyramidenspitze S auf der Leinwand. Die Eckpunkte \( B \) und C haben die Schattenpunkte \( B^{\prime}(7,5|0| 2) \) und \( C^{\prime}(2,5|0| 2) \). Zeigen Sie: Das Schattendreieck B C'S' ist ein gleichschenkliges Dreieck.
e) Zeigen Sie, dass der Vektor \( \vec{v} \) senkrecht auf der Dachfläche BCS steht.
\( \vec{v}=\left(\begin{array}{r} 0 \\ -2 \\ -1 \end{array}\right) \)
f) Ein Lichtstrahl in Richtung des Vektors \( \vec{v} \) erzeugt einen Schattenpunkt der Pyramidenspitze S. Liegt dieser Schattenpunkt auf der Bodenebene oder auf der Leinwand?
Problem/Ansatz
Ich verstehe nicht wie man auf s kommt
D-f verstehe ich auch komplett nicht