Ich habe folgende Ungleichung zu zeigen für n≥2:
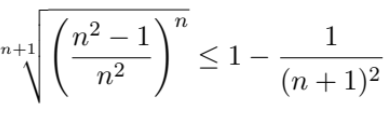
Text erkannt:
\( \sqrt[n+1]{\left(\frac{n^{2}-1}{n^{2}}\right)^{n}} \leq 1-\frac{1}{(n+1)^{2}} \)
Diese Ungleichung sollte mit der AM-Ungleichung abgeschätzt werden
Text erkannt:
\( \sqrt[n+1]{\left(\frac{n^{2}-1}{n^{2}}\right)^{n}} \leq 1-\frac{1}{(n+1)^{2}} \)
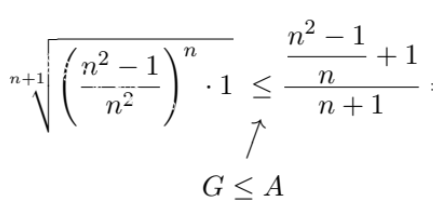
Text erkannt:
\( \begin{array}{l}\sqrt[n+1]{\left(\frac{n^{2}-1}{n^{2}}\right)^{n} \cdot 1} \leq \frac{\frac{n^{2}-1}{n}+1}{\uparrow} \\ G \leq A \\\end{array} \ Wie wird hier genau abgeschätzt. Der Nenner auf der rechten Seite ist mir kalr
Der Nenner auf der rechten Seite ist mir klar (also n+1), aber wie kommt der Zähler auf der rechten Seite zustande bei der Abschätzung?