Ich sollte eine Folge finden, die nicht konvergent ist und nur einen Häufungspunkt in R hat. Ich habe hier ein Beispiel gefunden, kann man das nehmen?
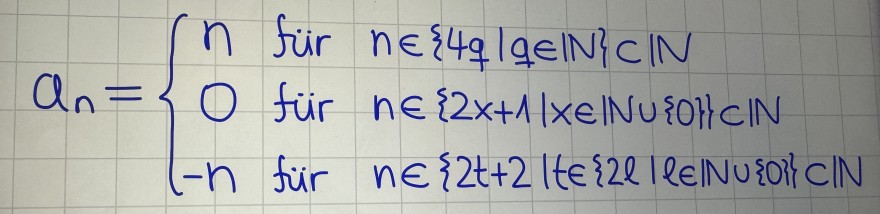
Text erkannt:
\( a_{n}=\left\{\begin{array}{rll}n & \text { für } & n \in\{4 q \mid q \in \mathbb{N}\} \subset \mathbb{N} \\ 0 & \text { für } & n \in\{2 x+1 \mid x \in \mathbb{N} \cup\{0\}\} \mathbb{N} \\ -n & \text { für } & n \in\{2 t+2 \mid t \in\{2 \ell \mid l \in \mathbb{N} \cup\{0\} \mathbb{N}\end{array}\right. \)