E Funktion Produkt Ableitung

Question

Aufgabe:

E Funktion Ableiten.

Problem/Ansatz:

Ich habe folgende die erste Ableitung von der Funktion gegeben:

Text erkannt:

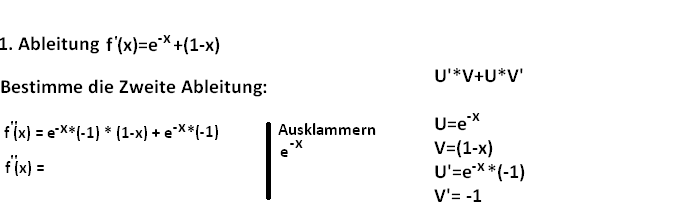
1. Ableitung \( f^{\prime}(x)=e^{-x}+(1-x) \)

Bestimme die Zweite Ableitung:
\( \begin{array}{l|ll} f^{\prime \prime}(x)=e^{-X *}(-1) *(1-x)+e^{-x *}(-1) & \text { Ausklammern } & U=e^{-x} \\ f^{\prime \prime}(x)= & e^{-x} & V=(1-x) \\ & & U^{\prime}=e^{-x *}(-1) \\ & V^{\prime}=-1 \end{array} \)
\( \mathrm{U}^{\prime *} \mathrm{~V}+\mathrm{U}^{*} \mathrm{~V}^{\prime} \)

Ausklammern

Ich habe ein Problem beim zusammenfassen:

Soll ich zunächst auf beide Seiten e-x* (-1) zusammenrechnen und des dann ausklammern? Siehe Abbildung

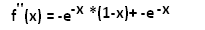
Text erkannt:

\( f^{\prime \prime}(x)=-e^{-x *}(1-x)+-e^{-x} \)

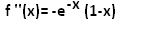
Text erkannt:

\( f^{\prime \prime}(x)=-e^{-x}(1-x) \)

Oder wie soll ich da vorgehen?

Comments

@DerHorst: Ich sehe hier drei verschiedene Varianten der Funktion, und drei Hilfswillige die versucht haben, Dir kostenlos zu helfen. Ich schlage vor, Du teilst erst mal klipp und klar mit, wie die Funktion nun wirklich lautet. Schreibe sie einfach hin.

---

Deine Zeile  \( f^{\prime \prime}(x)=-e^{-x}(1-x) - e^{-x} \)  ist noch richtig.
Wenn du dort e^-x ausklammerst, erhältst du f"(x) = e^-x·(-1+x-1) = e^-x·(x-2)

---

Okey, hier die Funktion: f(x)=x*ehoch-2

---

Sorry erstmal, falls ich undankbar rüber gekommen bin ich schätze die Kostenlose Hilfe enorm. Ich habe nicht wahrgenommen, dass man die Ursprungsfunktion wissen möchte. Das Nächste mal werde ich alle Informationen zu Verfügung stellen. Mich wundert es ,dass mein Professor fast jede Aufgabe falsch in seinem Buch hat. Auch hier hat er eine andere Lösung als du angegeben.

Text erkannt:

\( f^{\prime \prime}(x)=-\mathrm{e}^{-x}-(1-x) \mathrm{e}^{-x}=-(2-x) \mathrm{e}^{-x} \)

---

Okey, hier die Funktion: f(x)=x*ehoch-2

Das ist die vierte Variante. Und zwei Minuten später hast Du nochmals eine andere Funktion bestätigt mit "das stimmt".

---

Tippfehler, statt -2 -x. Sonst stimmt alles.

---

Niemand kann Dir helfen, wenn Du nicht in der Lage bist, die Funktion hinzuschreiben, für die Du die erste und zweite Ableitung suchst.

Wie lautet die Funktion (niemand wird das hier in der Auswahlsendung zusammensuchen können, abgesehen von Zufallstreffer), und was ist Deine Frage dazu?

---

Die Frage wurde von Gast hj2166 beantwortet. Die Frage war, wie das weitere Vorgehen beim zusammenfassen aussieht.

Ich sehe keine Möglichkeit die Frage als beantwortet zu markieren, sonst hätte ich das schon getan.

Answer 1

$$f'(x) = e^{-x} \cdot (1 - x) \newline \text{Ableitung mit Produkt und Kettenregel} \newline f''(x) = -e^{-x} \cdot (1 - x) + e^{-x} \cdot (-1) \newline f''(x) = e^{-x} \cdot (x - 1) + e^{-x} \cdot (-1) \newline f''(x) = e^{-x} \cdot (x - 2) \newline \text{Oder wie dein Prof es hatte} \newline f''(x) = - (2 - x) \cdot e^{-x} \newline$$

Comments

Kleiner Tipp: Eine Webseite wie http://www.ableitungsrechner.net ist ideal zur Hilfe und Selbstkontrolle.

Answer 2

Wenn die erste Ableitung oben so stimmt (wissen wir ja nicht), dann ist die zweite jedenfalls falsch. Du hast die Produktregel angewandt, aber warum heißt die wohl so? Hier (d.h. in der ersten Ableitung) liegt ja eine Summe vor, kein Produkt.

Answer 3

\( f'(x)=e^{-x}\red{+}(1-x) \)      

\( f''(x)=e^{-x}\cdot(-1)-1 \)

Achtung:

Dein angebener Weg ist nicht richtig!

Comments

Stimmt ,dass muss ein Mal sein kein plus. Aber dennoch sehe ich kein Fehler in der 2. Ableitung. Ich habe die Regel von U,V und U' und V' beachtet.

Answer 4

Du meinst wohl

f(x) = e^(-x)*(1-x)

u= e^(-x), u' = -e^(-x)

v= 1-x, v' = -1

f '(x) = -e^(-x)*(1-x)+ e^(-x)*(-1) = e^(-x)*(x-1-1) = e^(-x)*(x-2)

f ''(x):

u= e^(-x), u'= -e^(-x)

v= x-2, v' = 1

f ''(x) = ....

https://www.ableitungsrechner.net/

Comments

Die Ausgangsfunktion war nicht ehoch-x

sondern xehoch-1

---

sondern xehoch-1

du meinst sicher x·e^{-x}

---

Genau, das stimmt