Aufgabe:
Berechnung einer quartischen Funktion p(x) (hellgrüner Graph)
Problem/Ansatz:
Hallo liebe Mathefreunde,
ich hoffe sehr, dass ich mich noch einmal mit einer Aufgabe bei Euch melden darf.
Vielleicht hat ja jemand Lust, diese zu lösen.
a.)
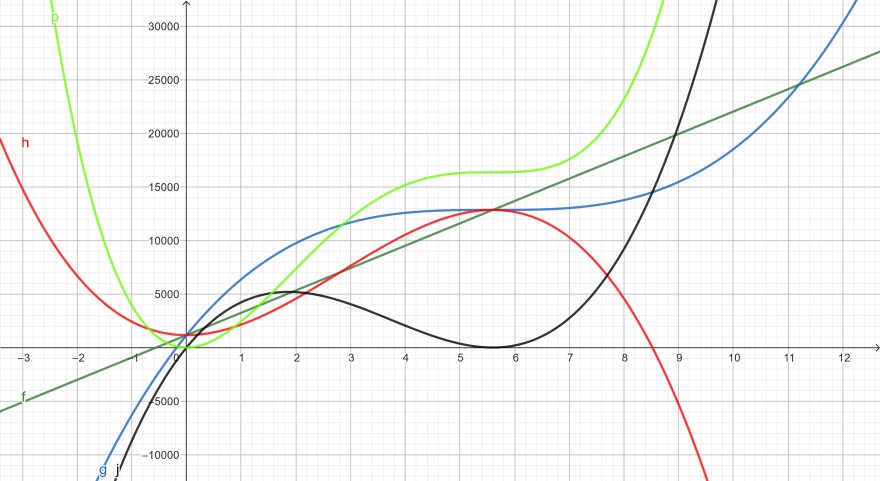
gegeben ist die lineare Funktion f(x) = 6272/3 x + 1159,2 (Gerade dunkelgrüner Graph)
b.)
1.) g(x) (blauer Graph) ist die erste kubische Funktion mit dem Sattelpunkt an der Stelle 5.6
g(0) = f(0) und g(5,6) = f(5,6)
2.) h(x) (roter Graph) ist die zweite kubische Funktion mit Extrempunkten an den Stellen 0 und 5,6
h(0) = f(0) und h(5,6) = f(5,6) sowie h´(0) und h´(5,6)
c.)
i(x) ist die Differenz zwischen g(x) und h(x) (schwarzer Graph) und hat Nullstellen bei 0 und 5,6
g(x) - h(x)
d.)
p(x) (hellgrüner Graph) ist die Stammfunktion von i(x)
die quartische Funktion p(x) hat sowohl einen Extempunkt an der Stelle 0 und gleichzeitig auch wieder einen Sattelpunkt an der Stelle 5,6.
Ich wünsche Euch allen ein schönes Osterfest.
mit freundlichen Grüßen aus Wesertal
Martin Hümer