Aufgabe:
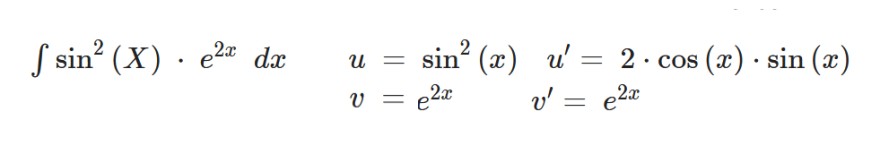
Text erkannt:
\( \begin{aligned} \int \sin ^{2}(X) \cdot e^{2 x} d x \quad u & =\sin ^{2}(x) \quad u^{\prime}=2 \cdot \cos (x) \cdot \sin (x) \\ v & =e^{2 x} \quad v^{\prime}=e^{2 x}\end{aligned} \)

Text erkannt:
Allgemeine Partielle Integration Formel:
\( u \cdot v-\int u^{\prime} \cdot v \)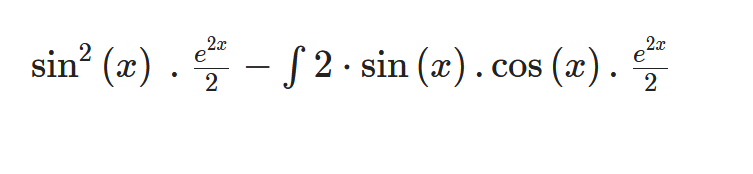
Text erkannt:
\( \sin ^{2}(x) \cdot \frac{e^{2 x}}{2}-\int 2 \cdot \sin (x) \cdot \cos (x) \cdot \frac{e^{2 x}}{2} \)
Problem/Ansatz:
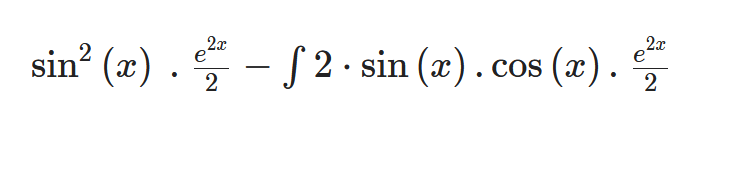
Text erkannt:
\( \sin ^{2}(x) \cdot \frac{e^{2 x}}{2}-\int 2 \cdot \sin (x) \cdot \cos (x) \cdot \frac{e^{2 x}}{2} \)
Ich komme da nicht weiter, bitte um hilfe