Text erkannt:
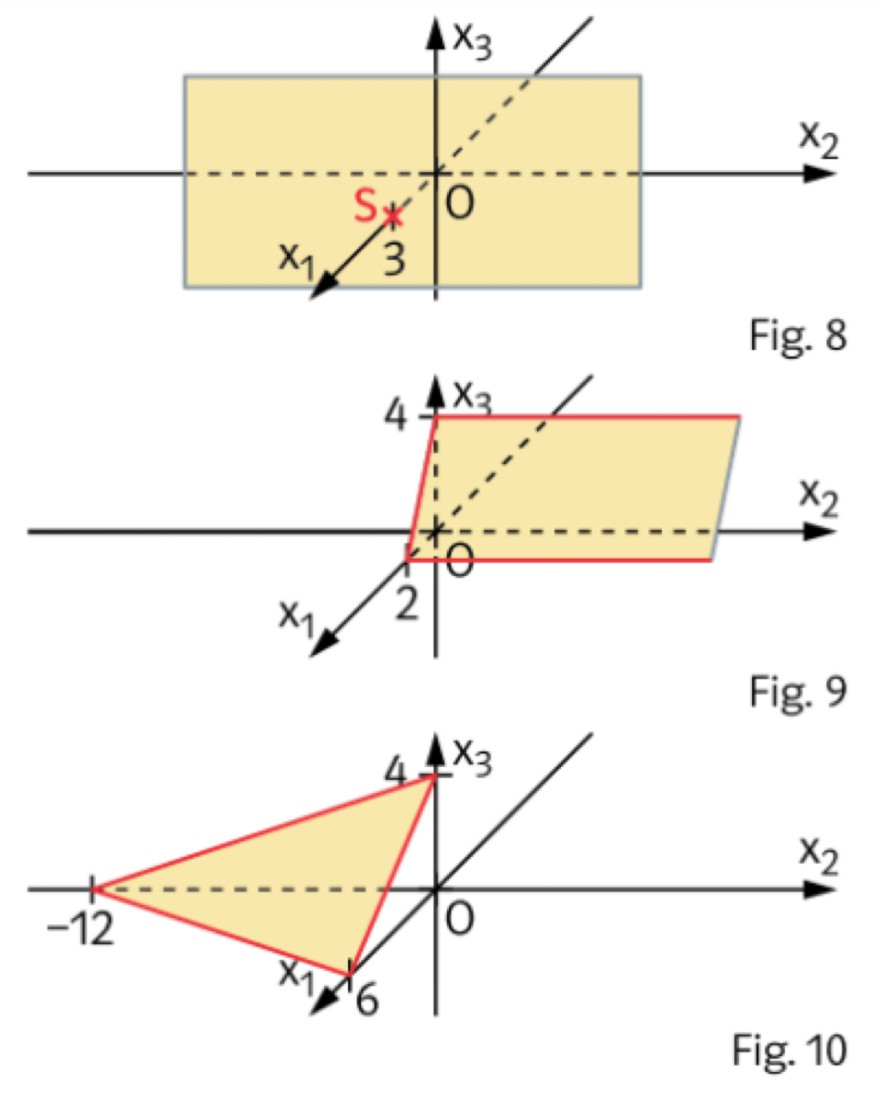
Fig. 8
Fig. 10
Aufgabe:
Welche Gleichungen passen zum abgebildeten Ebenenausschnitt? \\$$ a) I: x_1 = -3 \\ II: [\vec{x}-\left(\begin{array}{c} -3 & 0 & 0 \end{array}\right)] \cdot \left(\begin{array}{c} 1 & 0 & 0 \end{array}\right) = 0 \\ III: [\vec{x}-\left(\begin{array}{c} -3 & 2 & 1 \end{array}\right)] \cdot \left(\begin{array}{c} 0 & 0 & 1 \end{array}\right) = 0 \\ IV: \vec{x} = \left(\begin{array}{c} -3 & 0 & 0 \end{array}\right)+t \cdot \left(\begin{array}{c} 0 & 0 & 1 \end{array}\right)+s \cdot \left(\begin{array}{c} 0 & 1 & 0 \end{array}\right) \\ b) I: 2x_1 +x_3 = 4 \\ II: [\vec{x}-\left(\begin{array}{c} 2 & -1 & 2 \end{array}\right)]\cdot \left(\begin{array}{c} 4 & 0 & 2 \end{array}\right) = 0 \\ III: [\vec{x}-\left(\begin{array}{c} 2 & 0 & 1 \end{array}\right)]\cdot \left(\begin{array}{c} 2 & 0 & 1 \end{array}\right) = 0 \\ IV: \vec{x} = \left(\begin{array}{c} 2 & -1 & 2 \end{array}\right)+t \cdot \left(\begin{array}{c} 1 & 4 & -2 \end{array}\right)+s \cdot \left(\begin{array}{c} 1 & 3 & -2 \end{array}\right) \\ c) I: 2x_1 -x_2 +3x_3 = 12 \\ II: [\vec{x}-\left(\begin{array}{c} 0 & 0 & 4 \end{array}\right)] \cdot \left(\begin{array}{c} 2 & 1 & 3 \end{array}\right) = 0 \\ III: [\vec{x}-\left(\begin{array}{c} 0 & -12 & 0 \end{array}\right)] \cdot \left(\begin{array}{c} -4 & 2 & -6 \end{array}\right) = 0 \\ IV: \vec{x} = \left(\begin{array}{c} 3 & 0 & 2 \end{array}\right)+t \cdot \left(\begin{array}{c} 1 & 2 & 0 \end{array}\right)+s \cdot \left(\begin{array}{c} 1 & -1 & -1 \end{array}\right) $$
Problem/Ansatz:
Müsste in Fig. 8 der Schnittpunkt bei -3 sein anstelle von 3, wegen dem Stützvektor aus a) II? Gibt es noch weitere Fehler in dieser Aufgabe? Als Lösungen habe ich die Zuordnungen: Fig. 8 mit a), Fig. 9 mit b) und Fig. 10 mit c).