Text erkannt:
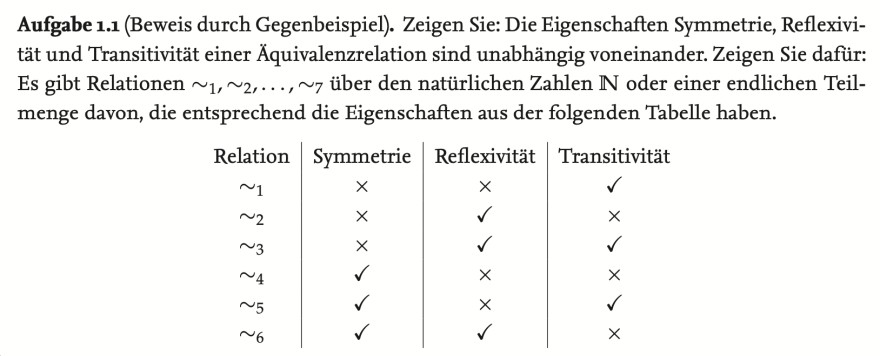
Aufgabe 1.1 (Beweis durch Gegenbeispiel). Zeigen Sie: Die Eigenschaften Symmetrie, Reflexivität und Transitivität einer Äquivalenzrelation sind unabhängig voneinander. Zeigen Sie dafür: Es gibt Relationen \( \sim_{1}, \sim_{2}, \ldots, \sim_{7} \) über den natürlichen Zahlen \( \mathbb{N} \) oder einer endlichen Teilmenge davon, die entsprechend die Eigenschaften aus der folgenden Tabelle haben.
\begin{tabular}{c|c|c|c}
Relation & Symmetrie & Reflexivität & Transitivität \\
\( \sim_{1} \) & \( \times \) & \( \times \) & \( \checkmark \) \\
\( \sim_{2} \) & \( \times \) & \( \checkmark \) & \( \times \) \\
\( \sim_{3} \) & \( \times \) & \( \checkmark \) & \( \checkmark \) \\
\( \sim_{4} \) & \( \checkmark \) & \( \times \) & \( \times \) \\
\( \sim_{5} \) & \( \checkmark \) & \( \times \) & \( \checkmark \) \\
\( \sim_{6} \) & \( \checkmark \) & \( \checkmark \) & \( \times \)
\end{tabular}
Problem/Ansatz: ich brauche Hilfe danke