Es ist günstiger, für Objekte unterschiedlicher Art auch unterschiedlichen Buchstabentypen zu verwnden. Bei dir werden f∈Hom(V,W) und g∈Hom(W,K) beide mit kleinen lateinischen Buchstaben bezeichnet, ich verwende gern folgende Schrifttypen :
und für die Abbildungen f, φ, ... die zugehörigen Abbildungsmatrizen F, Φ, .. , so dass man \( f(\vec v)=F·\vec v \) und \( ψ(\vec w)=Ψ·\vec w \) schreiben kann.
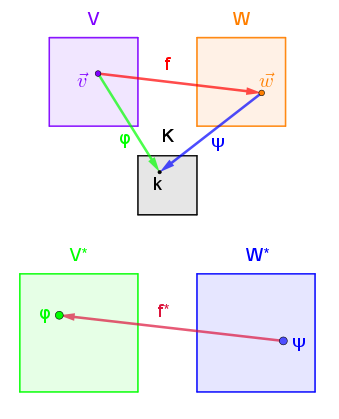
f* ist so definiert, dass f*(ψ) diejenige lineare Abbildung φ ist, die ein v auf diejenige Zahl k abbildet, welche das Bild von ψ angewendet auf f(v) ist : f*(ψ)(v) = ψ(f(v)). In Matrizenschreibweise wird daraus \(F^*·Ψ·\vec v=Ψ·F·\vec v\) bzw. F*·Ψ = Ψ·F.
Du schreibst völlig richtig, dass man um die Surjektivität von f* nachzuweisen zu jedem φ ein solches ψ angeben muss, das f*(ψ) = φ erfüllt, also eine solche Abbildungsmatrix Ψ, die F*·Ψ = Φ erfüllt, also die Ψ·F = Φ erfüllt. Ist nun für \(\vec v= \begin{pmatrix} x\\y \end{pmatrix} \) eine Abbildung φ durch \(φ(\vec v) = αx+βy\) , also die Abbildungsmatrix \(Φ= (α \; β)\) vorgegeben, so ist zur Bestimmung von \(Ψ =\begin{pmatrix} κ & λ & μ & ν \end{pmatrix} \) das Gleichungssystem \( \begin{pmatrix} κ & λ & μ & ν \end{pmatrix}· \begin{pmatrix} 1& 2 \\ 1 & 1 \\ 1 & -1 \\ 3 & 4 \end{pmatrix}=\begin{pmatrix} α &β \end{pmatrix}\) zu lösen.
Für den Kern von f* nehme man dann als φ die Nullabbildung ο mit ihrer Abbildungsmatrix \(Ο= \begin{pmatrix} 0 & 0 \end{pmatrix} \) .
Bemerkung :
Für die Surjektivität wird nur der Nachweis der Lösbarkeit (z.B. durch die Angabe irgendeiner Lösung) verlangt, für den Kern aber die Angabe aller Lösungen (Hinweis : die lassen sich als Linearkombinationen zweier Basislösungen angeben).