Bestimme die Funktionsgleichung der Funktion.

Question

Aufgabe: Hallo, ich habe probiert diese Aufgabe zu lösen, aber bin nie wirklich weitergekommen oder bin gescheitert und bräuchte dort etwas Hilfe um den Ansatz zu verstehen.

Problem/Ansatz:

1. Der Graph einer ganzrationalen Funktion vierten Grades ist achsensymmetrisch, hat eine
Nullstelle bei x=2, schneidet die y-Achse bei -4 und verläuft durch den Punkt P(1/9).
a) Bestimme die Funktionsgleichung der Funktion.
b) Berechne die fehlenden Nullstellen und stelle die Linearfaktordarstellung auf.

Ich hoffe ihr könntet mir da einen Schritt weiter helfen.

Answer 1

1. f(x)=ax^4+bx^2-4

f(2)=0 und f(1)=9 reicht zum

Bestimmen von a und b.

Answer 2

Hallo

achsensymmetrisch: nur gerade Potenzen also f(x)=ax^4+bx^2+c

dann f(2)=0; f(0)=-4, f(1)=5  gibt 3 Gleichungen um a,b,c zu bestimmen,

2. punktsym: nur ungerade Potenzen f(x)=ax^5+bx^3+cx , der Rest ähnlich wie 1. das x=0 Nullstelle sieht man direkt, dann für die 2 anderen Nst durch x≠0 teilen

Gruß lul

Answer 3

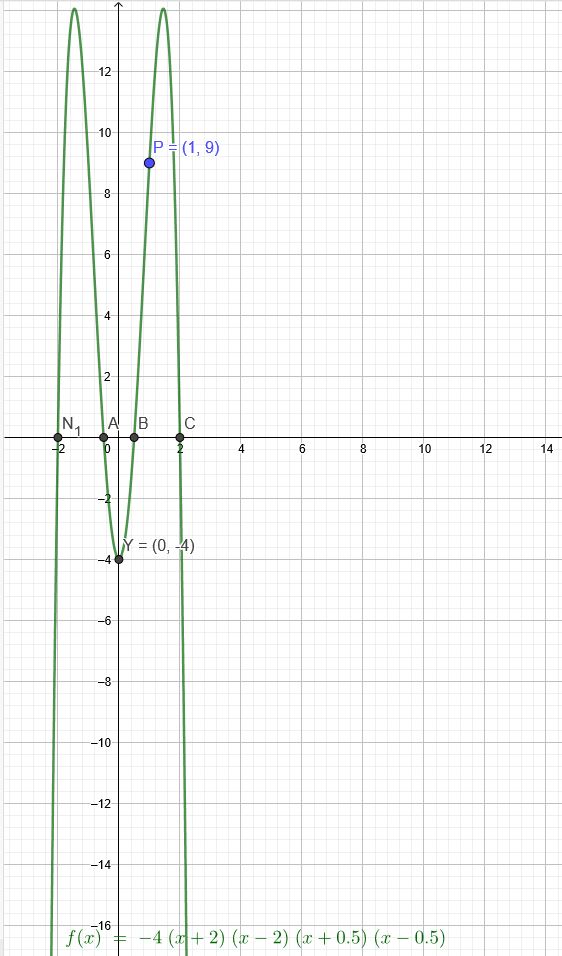
1. Der Graph einer ganzrationalen Funktion vierten Grades ist achsensymmetrisch, hat eine
Nullstelle bei \(x=2\) , schneidet die y-Achse bei -4 und verläuft durch den Punkt \(P(1|9)\).

Achsensymmetrie bedeutet, dass auch bei  \(x=-2\) eine Nullstelle ist:

\(f(x)=a(x-2)(x+2)(x-N)(x+N)=a(x^2-4)(x^2-N^2)\)

schneidet die y-Achse bei -4:

\(f(0)=a(0-4)(0-N^2)=4aN^2\)     \(4aN^2=-4\)   → \(a=-\frac{1}{N^2}\)

\(f(x)=-\frac{1}{N^2}(x^2-4)(x^2-N^2)\)

\(P(1|9)\):

\(f(1)=-\frac{1}{N^2}(1-4)(1-N^2)=\frac{3 \cdot (1-N^2)}{N^2}  \)

\(\frac{3 \cdot (1-N^2)}{N^2} =9 \)   →  \(\frac{ (1-N^2)}{N^2} =3 \)  →  \(N^2=0,25 \)      \(a=-4\)

\(f(x)=-4(x^2-4)(x^2-0,25)\)

\(f(x)=-4(x+2)(x-2)(x+0,5)(x-0,5)\)