Hallo, kann mir jemand bei dieser Aufgabe helfen?
Danke im Voraus.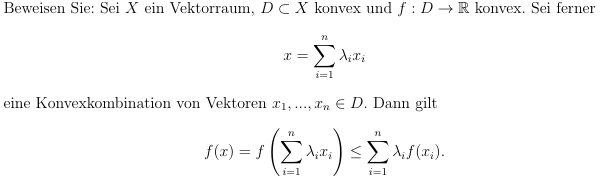
Text erkannt:
Beweisen Sie: Sei \( X \) ein Vektorraum, \( D \subset X \) konvex und \( f: D \rightarrow \mathbb{R} \) konvex. Sei ferner
\( x=\sum \limits_{i=1}^{n} \lambda_{i} x_{i} \)
eine Konvexkombination von Vektoren \( x_{1}, \ldots, x_{n} \in D \). Dann gilt
\( f(x)=f\left(\sum \limits_{i=1}^{n} \lambda_{i} x_{i}\right) \leq \sum \limits_{i=1}^{n} \lambda_{i} f\left(x_{i}\right) . \)