n über k richtige Formel?

Question

Ich habe einen Bitstring mit einhundert Einsen (111...)

Wie berechne ich die Anzahl der Möglichkeiten zwei Nullen in die Bitfolge einzufügen?

In unserem Buch gibt es folgende Formel:

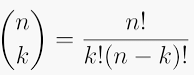
Text erkannt:

\( \binom{n}{k}=\frac{n!}{k!(n-k)!} \)

Wenn ich das richtig verstanden habe muss ich ja diese Formel verwenden oder?

Answer 1

Abändern. Also dass ich dann statt einer 1 eine o habe.

Ja. Das berechnest du korrekt mit

(100 über 2) = 100 * 99 / 2 = 50 * 99 = 4950

(100 über 2) = 100! / (2! * (100 - 2)!) = 4950

Beachte, dass du solche Dinge auch im hilfsmittelfreien Teil ohne Fakultät ausrechnen können solltest.

Answer 2

Einfügen oder abzuändern? Wenn du abänderst, suchst du zwei Stellen aus 100. Wenn du einfügst, suchst du 2 Stellen aus 102.

Hilft dir das weiter? Welche Bedeutung hat der Binomialkoeffizient?

Comments

Abändern. Also dass ich dann statt einer 1 eine o habe. Beispiel

Bitstring: 11111....

Nach dem abändern: 01101....

Die Bedeutung des binomialkoeffizienten ist ja dass ich k Elemente aus der Menge von n Elementen auswähle.(Reihenfolge egal) In meinem Fall ist doch dann 100 über 2 oder?

---

Wenn du einfügst, suchst du 2 Stellen aus 102.

(102 über 2) ist zwar als Formel richtig allerdings finde ich es ungünstig das mit 102 Stellen zu bezeichnen. Denn bei 100 Bits findest du eben keine 102 Stellen zum einfügen.

Besser wir fügen zwei Einsen dazu und wählen uns danach 2 Einsen aus, die wir durch Nullen ersetzen.

(100 + 2 über 2)

---

In meinem Fall ist doch dann 100 über 2 oder?

Korrekt.

Answer 3

Dann werden 102 Stellen draus.

(102 0ber 2) =  102!/(2!*100!) =  (102*101*100!)/(2*100!) = 102*101/2 = 5151