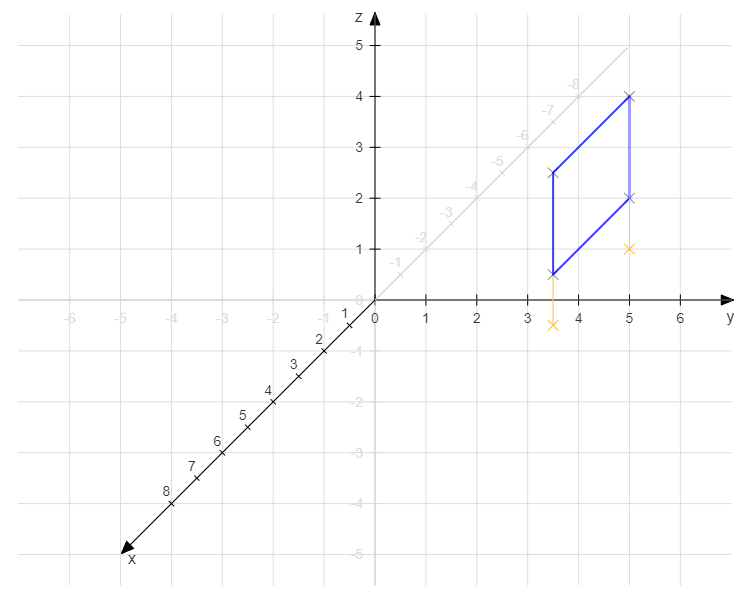
Gegeben sind die Punkte A(1,4,1), B (-2,4,1), C(-2,4,3). Das sind Eckpunkte eines Quadrats. Bestimmen Sie die Koordinaten von D.
Bei einem Rechteck (Quadrat) gilt, weil gegenüberliegende Seiten parallel und gleich lang sind:
AD = BC
D - A = C - B
D = A + C - B
Wir setzen ein
D = [1, 4, 1] + [-2, 4, 3] - [-2, 4, 1] = [1, 4, 3] → D(1 | 4 | 3)