Aufgabe:
Problem/Ansatz:
Hallo liebe Community,
gegeben ist folgende Funktion:
Foto 1
Zu dieser Funktion wurde als Grenzwert die Gaußsche Glockenkurve mit e^1/2*x^2 gefunden. Da die Funktion allerdings noch integriert wird, gilt dieser Grenzwert ja nicht zwangsläufig mit dem Integral weshalb dominierte Konvergenz verwendet wurde. Die Majorante dazu war:
Foto 2
Und dann wurde folgendes gemacht, was ich nicht ganz verstehe
Foto 3 und 4
anscheinend wurde durch Monotonieverhalten gezeigt, warum die Funktion immer kleiner als die Majorante ist, aber das verstehe ich nicht ganz. Kann mir bitte jemand erklären was auf den letzten beiden Fotos passiert ist?
Lg

Text erkannt:
\( \frac{(\sqrt{n} x+n)^{n} e^{-(\sqrt{n} x+n)}}{\left(\frac{n}{e}\right)^{n}} \)
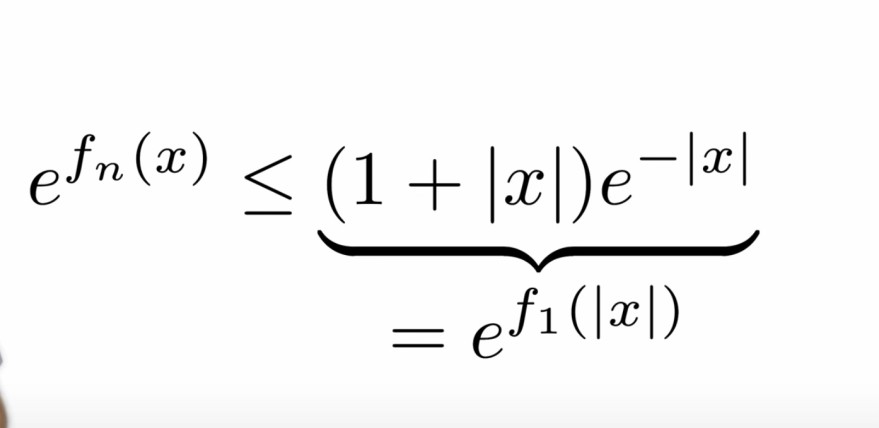
Text erkannt:
\( e^{f_{n}(x)} \leq \underbrace{(1+|x|) e^{-|x|}}_{=e^{f_{1}(|x|)}} \)

Text erkannt:
Sei \( h(x)=f_{n}(x)-f_{1}(|x|) \).
Für \( -\sqrt{n}<x<0 \) gilt
Für \( x>0 \) gilt
\( \begin{array}{l} h(x)=f_{n}(x)-f_{1}(-x) \quad h(x)=f_{n}(x)-f_{1}(x) \\ h^{\prime}(x)=f_{n}^{\prime}(x)+f_{1}^{\prime}(-x) \quad h^{\prime}(x)=f_{n}^{\prime}(x)-f_{1}^{\prime}(x) \\ =\frac{(1+\sqrt{n}) x^{2}}{\underbrace{(1-x)}_{\geq 0} \underbrace{(x+\sqrt{n})}_{\geq 0}} \\ =-\underbrace{\frac{(\sqrt{n}-1) x^{2}}{(x+1)} \underbrace{(x+\sqrt{n})}_{\geq 0}}_{\geq 0} \\ \geq 0 \text {. } \\ \leq 0 \text {. } \\ \end{array} \)
Somit ist \( h \) monoton
Somit ist \( h \) monoton steigend auf \( (-\sqrt{n}, 0) \). fallend auf auf \( (0, \infty) \).

Text erkannt:
Für alle \( x>-\sqrt{n} \) gilt also
\( \begin{aligned} h(x) & \leq h(0) \\ f_{n}(x)-f_{1}(|x|) & \leq 0 \\ f_{n}(x) & \leq f_{1}(|x|) \\ e^{f_{n}(x)} & \leq e^{f_{1}(|x|)} \\ e^{f_{n}(x)} & \leq(1+|x|) e^{-|x|} \end{aligned} \)