abgesehen davon, dass Q(0|-1) nicht auf dem Graphen von f(x) = e-x liegt, sondern stattdessen der Punkt Q(0|+1), kommen wir beide fast auf das gleiche Ergebnis:
Die Gleichung einer Tangente an den Graphen einer Funktion f(x) am Punkt (x0|f(x0)) lautet allgemein:
t(x) = f'(x0) * (x - x0) + f(x0)
Bestimmen wir die einzelnen Komponenten:
f(x) = e-x
f(0) = e-0 = 1
f'(x) = -1 * e-x
f'(0) = -1 * e-0 = -1
Wir setzen ein und erhalten:
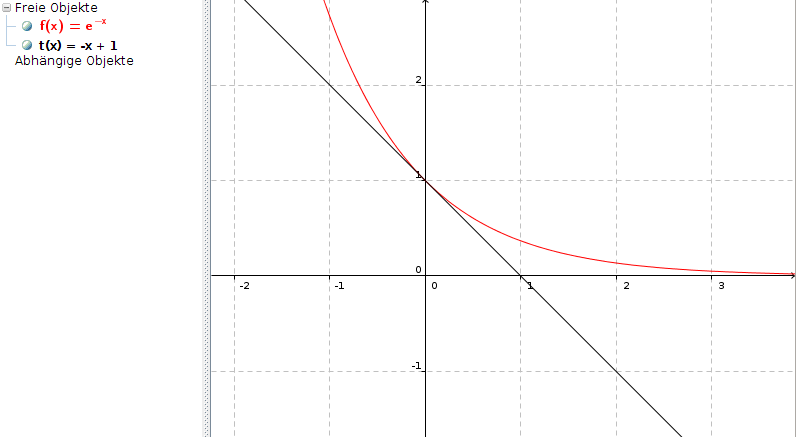
t(x) = -1 * (x - 0) + 1 = - x + 1
Besten Gruß