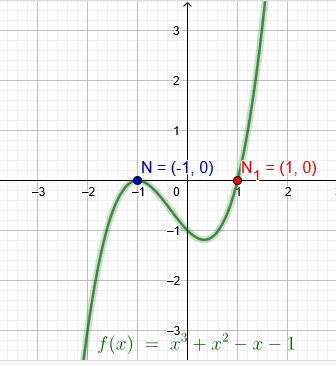
3) Polynomdivision: x= 1 ist geratene Nullstelle:
\((x^3+x^2-x-1) : (x-1)=x^2+2x+1\)
\(- (x^3-x^2) \)
------------------------
\(2x^2-x\)
\(- (2x^2-2x) \)
------------------------
\(x-1\)
\(-(x-1)\)
------------------------
\(0\)
\(x^2+2x+1=0\)
\((x+1)^2=0\)
\((x+1)^2=0\)
\(x=-1\) ist eine doppelte Nullstelle