Lage Beziehungen mithilfe des Normalenvektors untersuchen

Question

Aufgabe:

Lage Beziehungen mithilfe des Normalenvektors untersuchen

hello, ich muss im Unterricht ein Thema präsentieren um meine Note zur verbessern.
Das sind meine Ergebnisse:

Text erkannt:

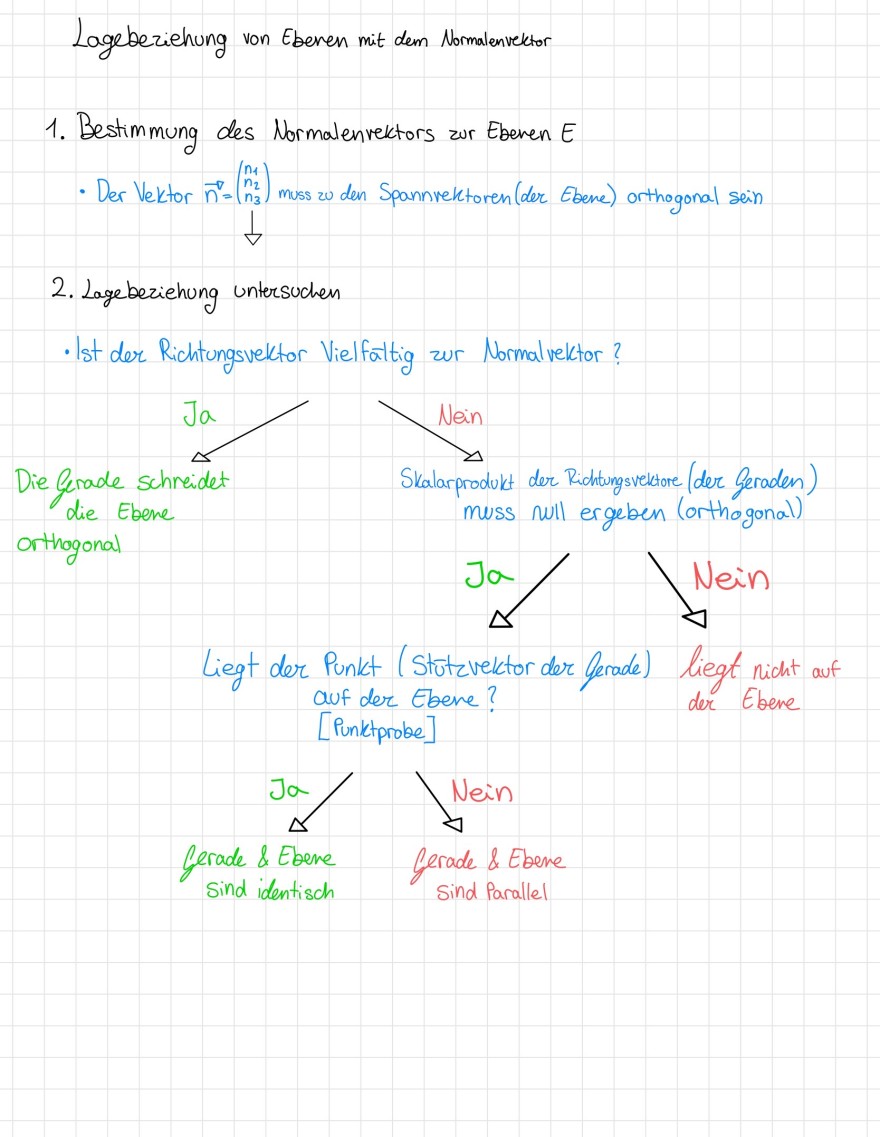
Lageberiehung von Eberen mit dem Normalenvector
1. Bestimmung des Normalenvektors zur Eberen E
- Der Vektor \( \vec{n}=\left(\begin{array}{l}n_{1} \\ n_{2} \\ n_{3}\end{array}\right) \) muss zu den Spannvektoren (der Ebene) orthogonal sein
2. Lageberiehung untersuchen
- Ist der Richtungsuektor Vielfältig zur Normalvektor?

Die Gerade schreidet die Ebene
Skalarprodukt der Richtungsvelutore (der Geraden) muss null ergeben (orthogonal) orthogonal
Liegt der Punkt (Stützvektor der Gerade) liegt nicht auf auf der Ebene? der Ebere [Punktprobe]
Ja
Nein
Gerade \& Ebere
Gerade \& Ebere
sind identisch
sind Parallel

Text erkannt:

Fig. 1 \( \vec{n}=\left(\begin{array}{r}-2 \\ 1 \\ 2\end{array}\right) \) ist nicht der einzige Normalenvektor der Ebene E. Weitere Normalenvektoren sind
z. B. \( \left(\begin{array}{r}-4 \\ 2 \\ 4\end{array}\right) \) oder \( \left(\begin{array}{r}2 \\ -1 \\ -2\end{array}\right) \)
Normalenvektor
Wenn die Gerade g und die Ebene E sich schneiden, kann zusätzlich untersucht werden, oD ale Gerade orthogonal zur Ebene liegt. Dies ist der Fall, wenn der Richtungsvektor der Geraden zu beiden Spannvektoren der Ebene orthogonal ist. Man nennt einen solchen Vektor, der orthogonal zur Ebene E ist, einen Normalenvektor der Ebene E.
Kennt man bereits einen Normalenvektor der Ebene \( E \), so kann die gegenseitige Lage der Geraden \( \mathrm{g} \) und der Ebene E mithilfe des Richtungsvektors \( \overrightarrow{\mathrm{u}} \) der Geraden \( \mathrm{g} \) und des Normalenvektors \( \vec{n} \) der Ebene E untersucht werden.
Wenn \( \vec{u} \) und \( \vec{n} \) Vielfache voneinander sind, schneidet die Gerade g die Ebene orthogonal (Fig. 1). Wenn \( \vec{u} \) und \( \vec{n} \) zueinander orthogonal sind, liegt \( g \) in E oder \( g \) ist parallel zu \( E \).
Lagebeziehungen mithilfe des Normalenvektors untersuchen
Gegeben sind die Geraden \( g: \vec{x}=\left(\begin{array}{l}1 \\ 2 \\ 3\end{array}\right)+t \cdot\left(\begin{array}{l}1 \\ 2 \\ 0\end{array}\right) \) und \( h: \vec{x}=\left(\begin{array}{l}2 \\ 3 \\ 5\end{array}\right)+t \cdot\left(\begin{array}{r}4 \\ -2 \\ -4\end{array}\right) \) sowie die Ebene \( E: \vec{x}=\left(\begin{array}{r}2 \\ -4 \\ 2\end{array}\right)+r \cdot\left(\begin{array}{l}1 \\ 0 \\ 1\end{array}\right)+s \cdot\left(\begin{array}{r}2 \\ -2 \\ 3\end{array}\right) \)
1. Bestimmen des Normalenvektors zur Ebene \( E \)
Der Vektor \( \vec{n}=\left(\begin{array}{l}n_{1} \\ n_{2} \\ n_{3}\end{array}\right) \) muss zu den Spannvektoren \( \left(\begin{array}{l}1 \\ 0 \\ 1\end{array}\right) \) und \( \left(\begin{array}{r}2 \\ -2 \\ 3\end{array}\right) \) orthogonal sein.
Es muss gelten \( \left(\begin{array}{l}n_{1} \\ n_{2} \\ n_{3}\end{array}\right) \cdot\left(\begin{array}{l}1 \\ 0 \\ 1\end{array}\right)=0 \) und \( \left(\begin{array}{l}n_{1} \\ n_{2} \\ n_{3}\end{array}\right) \cdot\left(\begin{array}{r}2 \\ -2 \\ 3\end{array}\right)=0 \). Dies führt auf das LGS \( \begin{array}{r}n_{1} \\ 2 n_{1}-2 n_{2}+3 n_{3}=0\end{array} \). Eine Lösung dieses LGS ist \( (-2 ; 1 ; 2) \), also ist \( \vec{n}=\left(\begin{array}{r}-2 \\ 1 \\ 2\end{array}\right) \) ein möglicher Normalenvektor der Ebene E.
2. Lagebeziehungen untersuchen
Das Skalarprodukt des Richtungsvektors von g mit \( \vec{n} \) lautet: \( \left(\begin{array}{l}1 \\ 2 \\ 0\end{array}\right) \cdot\left(\begin{array}{r}-2 \\ 1 \\ 2\end{array}\right)=0 \). Somit sind die
Vektoren zueinander orthogonal. Die Gerade g liegt in der Ebene E oder ist parallel zu ihr. Die Punktprobe ergibt, dass der Geradenpunkt \( P(1|2| 3) \) nicht auf der Ebene E liegt.
Also sind \( g \) und E zueinander parallel.
Wegen \( \left(\begin{array}{r}4 \\ -2 \\ -4\end{array}\right)=-2 \cdot\left(\begin{array}{r}-2 \\ 1 \\ 2\end{array}\right) \) sind die Richtungsvektoren von \( h \) und der Normalenvektor \( \vec{n} \) Vielfache voneinander. Die Gerade h schneidet die Ebene E orthogonal.

Ich habe dafür diese internetseite benutzt: (oben)

Die Seite war relativ schwer (meiner Meinung nach) erklärt und habe deswegen Angst, dass ich etwas falsch verstanden hab. Könnte jemand bitte ein Blick darauf werden. Danke im Voraus

Comments

Bereits die Überschrift ist falsch. Es geht nicht um die Lagebeziehung von Ebenen, sondern um die Lagebeziehung einer Geraden zu einer Ebene.

Es wäre gut, wenn du es tatsächlich auch an einem konkreten Beispiel vormachst.

Normal prüft man zuerst, ob das Skalarprodukt aus Richtungs- und Normalenvektor gleich null ist.

Gerade und Ebene können nicht identisch sein. Besser ist die Gerade liegt in der Ebene.

Wenn das Skalarprodukt ungleich null ist dann schneidet die Gerade die Ebene. Dann kannst du evtl. überprüfen, ob das schneiden senkrecht geschieht. Meist ist das aber uninteressant in welchem Winkel die Gerade die Ebene schneidet. Das Gehört zur Lageuntersuchung normalerweise nicht mit dazu. Aber im Buchbeispiel wurde das eben auch untersucht.

Answer 1

Passe mit den Begrifflichkeiten genau auf. Das wurde dir ja im Kommentar oben schon erläutert.

Zu 1.)

Führe an dieser Stelle auch auf, wie man den Normalenvektor berechnet. Wenn du es präsentieren sollst, bietet sich eine Skizze an (siehe Buch), wo man sehen kann, warum der Normalenvektor senkrecht auf den Spannvektoren stehen muss.

Wenn du noch eins draufsetzen möchtest, recherchiere mal nach Vektorprodukt oder Kreuzprodukt. Das ist nämlich die schnellere und einfachere Methode, einen Normalenvektor zu berechnen, da man damit sofort einen Vektor berechnen kann, der senkrecht auf den zwei gegebenen Vektoren steht.

Zu 2.)

In erster Linie interessiert dich, ob der Richtungsvektor orthogonal zum Normalenvektor ist. Wenn ja, dann liegt die Gerade entweder in der Ebene oder nicht. Das prüft man dann mit einer Punktprobe. Wenn nicht, kann man zusätzlich prüfen, ob die Gerade die Ebene orthogonal schneidet oder nicht, muss man aber nicht. Allerdings kann man ja sofort erkennen, ob der Normalenvektor ein Vielfaches des Richtungsvektors ist. Der Fachbegriff lautet übrigens kollinear.