Zeigen Sie, dass f in (0,0) nicht differenzierbar ist.

Question

Aufgabe: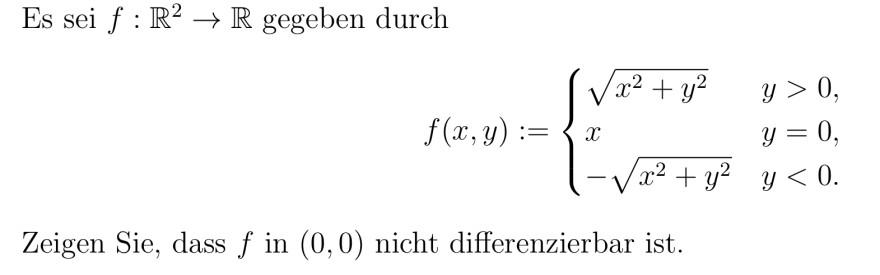

Text erkannt:

Es sei \( f: \mathbb{R}^{2} \rightarrow \mathbb{R} \) gegeben durch
\( f(x, y):=\left\{\begin{array}{ll} \sqrt{x^{2}+y^{2}} & y>0 \\ x & y=0 \\ -\sqrt{x^{2}+y^{2}} & y<0 . \end{array}\right. \)

Zeigen Sie, dass \( f \) in \( (0,0) \) nicht differenzierbar ist.

Problem/Ansatz:

Könnte mir jemand helfen, ob ich den richtigen Ansatz habe?

Ich hätte zuerst die Stetigkeit im Punkt (0,0) überprüft, indem ich den lim. für y<0, y=0 und y>0 untersuche. In diesem Fall wäre dieser immer 0, somit müsste Stetigkeit in den Punkt vorliegen.

Als Nächstes würde ich die Differenzierbarkeit untersuchen. Dafür würde ich die partielle Ableitung von f nach x und y bestimmen. Da weiß ich aber leider nicht wie die aussähe. Wären die partiellen Ableitungen verschieden, wäre due Funktion in f doch nicht diffbar oder?

Habe ich die richtige Idee zur Lösung der Aufgabe? Über Hilfe würde ich mich sehr freuen!

Comments

Hallo

was kannst du an den partiellen Ableitungen nicht?

fx=x/√(x^2+y^2) für y>0 entsprechend die anderen.

du musst erst mal untersuchen wie die einzelnen Ableitungen bei0 aussehen

lul

---

Text erkannt:

Jar \( y>0 \).
\( \begin{array}{ll} \frac{\partial f}{\partial x}\left(\sqrt{x^{2}+y^{2}}\right)=\frac{x}{\sqrt{x^{2}+y^{2}}} & \frac{\partial f}{\partial x}(0,0)=\frac{0}{\sqrt{0^{2}+0^{2}}}=0 \\ \frac{\partial f}{\partial y}\left(\sqrt{x^{2}+y^{2}}\right)=\frac{y}{\sqrt{x^{2}+y^{2}}} & \frac{\partial f}{\partial y}(0,0)=\frac{0}{\sqrt{0^{2}+0^{2}}}=0 \end{array} \)
für \( y=0 \) :
\( \begin{array}{l|l} \frac{\partial f}{\partial x}(x)=1 & \frac{\partial f}{\partial x}(0,0)=1 \\ \frac{\partial f}{\partial y}(x)=0 & \frac{\partial f}{\partial y}(0,0)=0 \end{array} \)
für \( y<0 \) :
\( \begin{array}{ll} \frac{\partial f}{\partial x}\left(-\sqrt{x^{2}+y^{2}}\right)=-\frac{x}{\sqrt{x^{2}+y^{2}}} & \frac{\partial f}{\partial x}(0,0)=-\frac{0}{\sqrt{0^{2}+0^{2}}}=0 \\ \frac{\partial f}{\partial y}\left(-\sqrt{x^{2}+y^{2}}\right)=-\frac{y}{\sqrt{x^{2}+y^{2}}} & \frac{\partial f}{\partial y}(0,0)=0 \end{array} \)

Ich habe mich nochmal an den partiellen Ableitungen versucht und geguckt, wie diese bei (0,0) aussehen. Passt das denn so bzw. was wäre der nächste Schritt?

Answer 1

Wie kommst du bei fx(0) auf =0 wenn du etwa auf der Geraden x=y nach 0 läufst hast du x/(√2x)auf anderen Wegen andere Werte!