Mehrdimensionale Integration Normalbereiche

Question

Die Menge \( B \subset \mathbb{R}^2 \) sei das Flächenstück zwischen der \( x \)-Achse und der Funktion \( y = e^x \) im Bereich \( x \in [0, 1] \).

(a) Skizzieren Sie die Menge \( B \) und stellen Sie sie anschließend zweimal als Normalbereich dar: einmal bzgl. der \( x \)-Achse und ein weiteres mal bzgl. der \( y \)-Achse.
Hinweis: Den Normalbereich bzgl. der \( y \)-Achse können Sie als Vereinigung zweier Normalbereiche schreiben, von denen einer rechteckig ist.

(b) Bestimmen Sie das Integral
\( \iint_B (x - \ln(y)) \, d(x, y) \)
zweimal, indem Sie jeweils einen Ihrer beiden Normalbereiche aus Teil (a) zugrundelegen.

Hinweis: Die Stammfunktion von \(\ln(y)\) lautet \(y(\ln(y) - 1)\), die von \((\ln(y))^2\) lautet
\(y((\ln(y))^2 - 2\ln(y) + 2)\)

Comments

Was hast du gemacht? Was kannst du nicht?

lul

---

ich bin mir der Lösung nicht sicher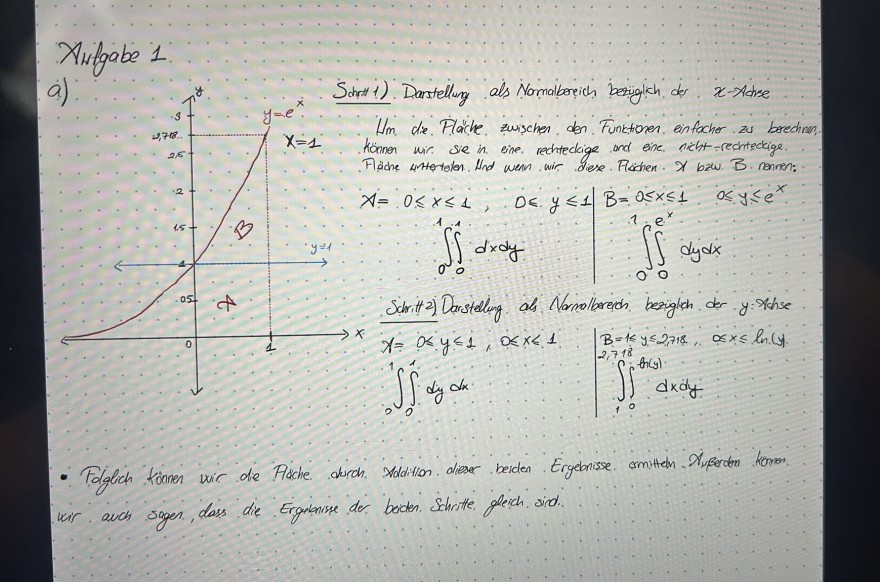

Text erkannt:

Xifgabe 1
- Tolglich Komnen vir de Aache durch Xddition diess beiden Ergebnisse omittän Xuferdön kommon wir auch soger, dass die Ergimisse der boiden Schotte gleich sidd

Text erkannt:

b)
(1) Der Narmalbercich bezuglich der \( x \)-xichse ist:
\( 0 \leqslant x<1 \quad 0 \leqslant y \leqslant e^{x} \)
- Das Integral lautert
- Uha hir wissen wir, dass: \( \int \ln (y) d y=y(\ln (y)-1) \)
Sanit:

Jetzt setzen vir alle zuammen:
\( \int \limits_{0}^{x^{x}}(x-\ln (y)) d y=x e^{x}-e^{x}(x-1)=x e^{x}-e^{x} x+e^{x} e^{x} \)

Text erkannt:

(2) Do Normalberech beruglich der y-Xche ist Hor tomen wir auch zwee Flicher monterteibe Dont Komm wir sogon deas.
\( \begin{array}{l} B=\left\{(x, y) \in \mathbb{R}^{2} \mid 0 \leq y \leq 1,0 \leq x \leq 1\right\} \cup\left\{(x, y) \in \mathbb{R}^{2} \mid 1 \leq y \leq e, \ln (y) \leq x \leq 1\right\} \\ \int \limits_{0}^{1} \int \limits_{0}^{1}(x-\ln (y)) d x d y+\int \limits_{1}^{e} \int \limits_{1}^{1}(x-\ln (y)(y)) d x d y \\ =\int \limits_{0}^{1} x d x-\int \limits_{0}^{1} \ln (y) d x+\int \limits_{\ln (y)}^{1} x d x-\int \limits_{\ln (y)}^{1} \ln (y) d x \\ =\frac{1}{2}-\ln (y)+\frac{1}{2}-\frac{\left(\ln (y)^{2}\right.}{2}-\left(\ln (y)-(\ln (y))^{2}\right) \\ -\int \limits_{0}^{1}\left(\frac{1}{2}-\ln (y)\right) d y+\int \limits_{1}^{e}\left(\frac{1}{2}-\frac{\left(\ln (y)^{2}\right.}{2}+\ln (y)\right) d y \\ =\frac{1}{2} \int \limits_{0}^{1} d y-\int \limits_{0}^{1} \ln (y) d y+\frac{1}{2} \int \limits_{1}^{1} d y-\frac{e}{1} \frac{\ln (y))^{2}}{2} d y+\int \limits_{1}^{e} \ln (y) d y \\ =\frac{1}{2}-\left([\dot{y}(\ln (y)-1)]_{0}^{1}\right)+\frac{1}{2}(e-1)-\frac{e}{2}+1 \\ =\frac{1}{2}-(-1) \\ =\frac{3}{2}+\frac{1}{2}=\frac{4}{2}=2 \\ \end{array} \)
\( Q \)
Q
\( \otimes \)
(
\( \sqrt{18} \)
圂
0
(2)
8

Text erkannt:

I Xißaden mbicht idh auch hier zogen. wie hode ah berechnat
\( -\int \limits_{1}^{e} \frac{(\ln (y))^{2}}{2} d y \Rightarrow \) Wir wissen dass \( \int(\ln (y))^{2} d y=y\left((\ln (y))^{2}-2 \ln (y)+2\right)+c \) \( =\frac{1}{2}(\ln (y))^{2} d y=\frac{1}{2}\left[y\left((\ln (y))^{2}-2 \ln (y)+2\right]_{1}^{e}\right. \)
\( \left.=\left[e\left((\ln (e))^{2}-2 \ln (e)+2\right)\right]-\left[1\left((\ln (1))^{2}-2 \ln (1)-2\right)\right] \quad\right] \ln (1)=0 \)
\( =\frac{1}{2}[e(1-2+2)] \)
\( =\frac{e}{2} \)
\( \begin{array}{l} -\int \limits_{1}^{e} \ln (y) d y-[y \ln (y)-y]_{1}^{e}=[e \ln (e)-e]-[1 \ln (1)-1] \\ =e 1-e-(0-1) \\ =1 \end{array} \)

Answer 1

Ich weiß nicht wie genau Normalbereich definiert ist und wie Ihr das aufschreibt. Es muss aber in beiden Fällen aufgeteilt werden in zwei Bereiche.

Der richtige Bereich für B ist \(\int\limits_1^e\int\limits_{\ln y}^1 dxdy\).

2.718 hat da nichts zu suchen und beim x-Integral sind die Grenzen andersrum.

Aus Deiner unübersichtlichen Rechnung (warum nicht getrennt über A und über B integrieren?) kann ich nicht sehen, wo Dein Fehler ist. Auf jeden Fall darfst Du auftretende Definitionslücken nicht einfach ignorieren (daher aufteilen).

Für das Integral über A erhalte ich \(1.5\).

Für das Integral über B \(e-2.5\).