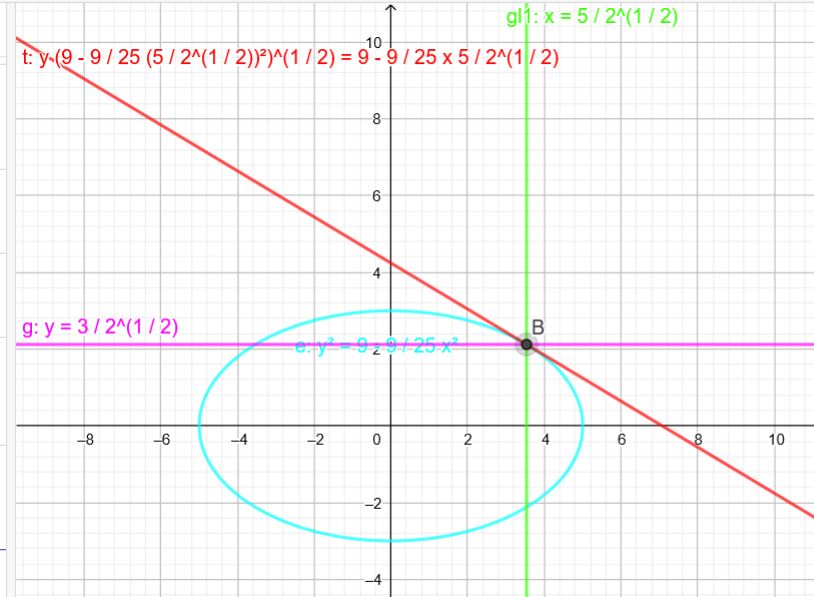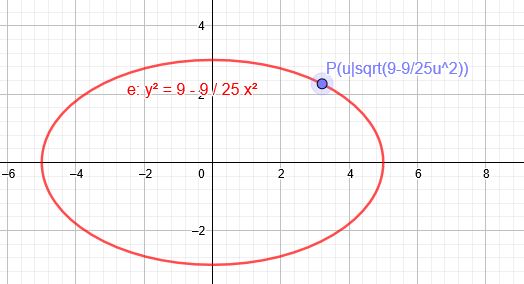
Tangentengleichung:
\(y\cdot\sqrt{9-\frac{9}{25}u^2}=9-\frac{9}{25}x\cdot u \)
Schnitt mit der x-Achse:
\(0\cdot\sqrt{9-\frac{9}{25}u^2}=9-\frac{9}{25}x\cdot u \)
\(9-\frac{9}{25}x\cdot u=0\)
\(\frac{9}{25}x=\frac{9}{u}\)
\(x=\frac{25}{u}\)
Schnitt mit der y-Achse:
\(y\cdot\sqrt{9-\frac{9}{25}u^2}=9-\frac{9}{25}\cdot 0\cdot u=9 \)
\(y=\frac{9}{\sqrt{9-\frac{9}{25}u^2}} \)
\(A(u)=0,5\cdot \frac{25}{u}\cdot \frac{9}{\sqrt{9-\frac{9}{25}u^2}} \)
\(A'(u)=0 \)
\(u=\frac{5}{\sqrt{2}} \)
\(x=\frac{5}{\sqrt{2}} \)
\(y^2=9- \frac{9}{25}x^2 \) \(y^2=9- \frac{9}{25} \cdot (\frac{5}{\sqrt{2}})^2=\frac{9}{2} \)
\(y=\frac{3}{\sqrt{2}} \)
Tangentengleichung:
\(y\cdot\sqrt{9-\frac{9}{25} \cdot (\frac{5}{\sqrt{2}})^2}=9-\frac{9}{25}x\cdot \frac{5}{\sqrt{2}} \)