Wie lautet der Rechenweg um bei b) auf 304 zu kommen?

Question

Text erkannt:

Haufig verkaufen Fluggesellschaften mehr Tickets für ihre Fluge, als Platze vorhanden sind, da meist einige Personen, die den Flug gebucht haben, die Reise nicht antreten. Für einen Flug mit 304 Sitzplatzen wurden 348 Tickets verkauft, die nicht storniert oder umgebucht werden können. Da es sich um eine Flugstrecke handelt, die im Regelfall von alleinreisenden Geschäftsleuten genutzt wird, nehmen wir an, dass alle Passagieren die Reise unabhängig voneinander jeweils mit Wahrscheinlichkeit \( p=0.86 \) antreten.
a) Bestimmen Sie die Wahrscheinlichkeit, dass niemand am Gate zuruckgelassen werden muss, mithilfe einer Normalapproximation ohne Stetigkeitskorrektur.

Hinweis: Sie müssen am Ende Ihrer Rechnung einen Wert \( \Phi(x) \) aus einer Quantilstabelle ablesen. Runden Sie dazu \( x \) auf genau zwei Nachkommastellen und tragen Sie die zugehörige aus der Quantilstabelle abgelesene, ungerundete Zahl mit vier Nachkommastellen in das Ergebnisfeld ein.
Die Wahrscheinlichkeit beträgt 0.7673
Ihre letzte Antwort wurde folgendermaßen interpretiert:
0.7673
b) Was ist die niedrigste Anzahl an Sitzplatzen, die das Flugzeug haben müsste, wenn die Wahrscheinlichkeit, dass im obigen Fall niemand am Gate zurückgelassen werden muss, mindestens \( \pi=0.75 \) betragen soll? Rechnen Sie emeut ohne Stetigkeitskorrektur.
Hinweis: Benutzen Sie für diese Teilaufgabe die unten stehende Quantilstabelle. Verwenden Sie den dort abgelesenen Wert mit drei Nachkommastellen.
Die Zahl der Sitzplatze müste mindestens 261
Ihre letzte Antwort wurde folgendermaBen interpretiert:
261

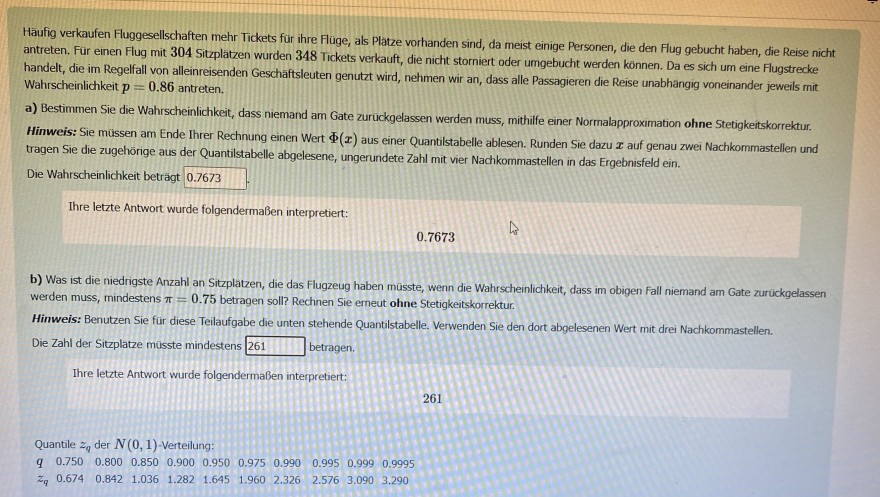
Quantile \( z_{q} \) der \( N(0,1) \)-Verteilung:
\( \begin{array}{lllllllllll}q & 0.750 & 0.800 & 0.850 & 0.900 & 0.950 & 0.975 & 0.990 & 0.995 & 0.999 & 0.9995 \\ z_{q} & 0.674 & 0.842 & 1.036 & 1.282 & 1.645 & 1.960 & 2.326 & 2.576 & 3.090 & 3.290\end{array} \)

Aufgabe:

Aufgabe a) ist richtig

Problem/Ansatz:

Wie lautet der Rechenweg um bei b) auf 304 zu kommen?

Denn bei b) ist 304 statt 261 richtig.

Comments

Ergebnis mit der Binomialverteilung zum Vergleich:

Es dürfen höchstens 304 kommen:

P(X<=304) = 1-P(X>=305) = 1- Σ k= 305 bis 348 (348 über k)*0,86^k*0,14^(348-k) = 0,788147757077

---

Das nutzt so gut wie nichts. Du hättest zusätzlich P(X<=303) auswerten müssen.

---

Es nutzt vor allem deswegen nichts, weil die Frage des FS - mal wieder - völlig ignoriert wird. Was will man hier mit einem Vergleichsergebnis?

---

Ein Vergleichsergebnis ist gut, allerdings hat der FS dies ja bereits gehabt

Wie lautet der Rechenweg um bei b) auf 304 zu kommen?
Denn bei b) ist 304 statt 261 richtig.

Die Frage ist, wie man auf 261 kommt, wenn im Mittel etwa 299 Personen zum Flug erscheinen. Dann würden 299 Platze gerade mal zu etwas über 50% reichen und nicht zu 75%

---

Warum fuscht man hier schon wieder an der Frage herum? Es ist durchaus gut zu wissen, was in Teil a) gefragt wird und dass der FS diese schon gelöst hat. Kann man nicht einfach mal die Finger von sowas lassen, vor allem dann, wenn sich bereits Antworten darauf beziehen!

Answer 1

Suche das passende Quantil \(z_q\) aus der Tabelle für \(q=0,75\) und löse \(\frac{z-\mu}{\sigma}=z_q\). Wobei \(\mu\) und \(\sigma\) Erwartungswert bzw. Standardabweichung sind.

Anhand der Aufgabe zuvor, kann man aber auch schon sehen, dass die 75 % mit den vorgegebenen 304 Sitzplätzen gerade so überschritten sind. Man könnte also auch einfach testen, ob man mit 303 Plätzen auch noch über diese 75 % kommt. Wenn nicht, ist \(n=304\).

Answer 2

b)

n = 348 ; p = 0.86

μ = n·p = 348·0.86 = 299.28
σ^2 = n·p·q = 348·0.86·0.14 = 41.8992

P(X ≤ k) = NORMAL((k - 299.28)/√41.8992) = 0.75
(k - 299.28)/√41.8992 = 0.674 → k = 303.6427744 → k = 304