f(x) = ax4 + bx3 + cx2 + dx + e
f'(x) = 4ax3 + 3bx2 + 2cx + d
f''(x) = 12ax2 + 6bx + 2c
f'''(x) = 24ax + 6b
f''(x) = x2 - 4 | => 12a = 1; 6b = 0; 2c = -4 | a = 1/12 ; b = 0 ; c = -2
f(x) = 1/12 * x4 - 2x2 + dx + e
f'(x) = 1/3 * x3 - 4x + d
f''(x) = x2 - 4
f'''(x) = 2x
f'(0) = 0 | => d = 0
f(-2) = 0 = 16/12 - 8 + e |
e = -16/12 + 96/12 = 80/12 = 20/3
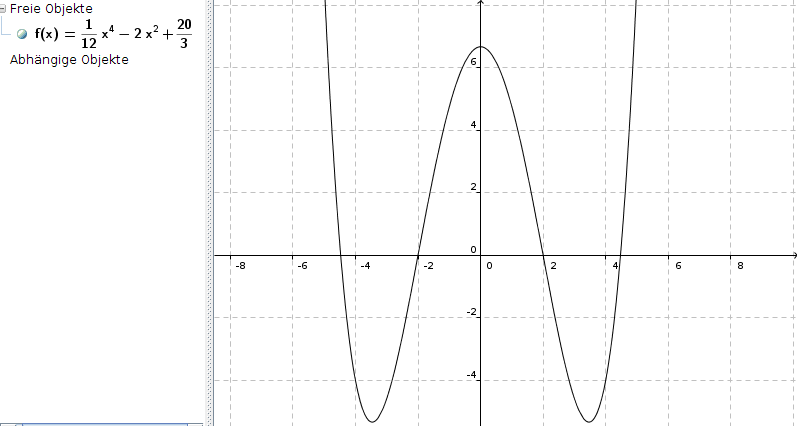
f(x) = 1/12 * x4 - 2x2 + 20/3
Besten Gruß