Gegeben war die Kurve c: [-1,1] -> R^2
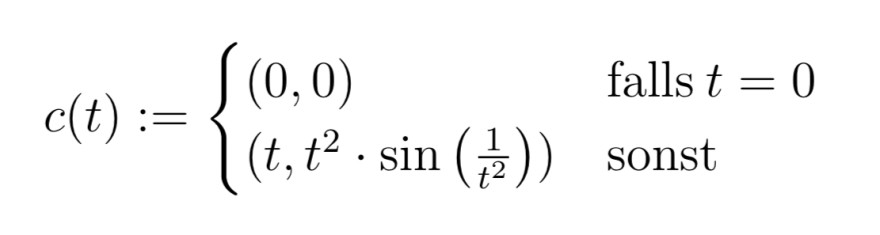
Text erkannt:
\( c(t):=\left\{\begin{array}{ll}(0,0) & \text { falls } t=0 \\ \left(t, t^{2} \cdot \sin \left(\frac{1}{t^{2}}\right)\right) & \text { sonst }\end{array}\right. \)
Also sie ist auf [-1,1] definiert.
Meine Aufgabe war es, zu zeigen, das c nicht rektifizierbar ist, d.h. die Länge der Kurve unendlich ist.
Ich habe es folgenderweise gemacht:

Text erkannt:
Definiere die Parhion(folge) \( T_{n}:=\{-1.0\} \cup\left\{\left.\frac{1}{\sqrt{k \pi} \pi} \right\rvert\, k=1 \ldots . . ..\right\} \cup\{1\} \) des Inlervalls [-1,1].
Dann gilt \( L(c)=\sup \left\{\sum \limits_{k=1}^{n}\left\|c\left(t_{k}\right)-c\left(t_{k-1}\right)\right\| \mid T=\left\{t_{0}, \ldots . t_{n}\right.\right. \) ist Parrhion von \( \left.[a b\}\right\} \)
\( \begin{array}{l} \text { da } \sin (k \pi)=0 \quad \forall k] \\ \geqslant \sum \limits_{k=2}^{n} \underbrace{\frac{1}{(k-1) \pi}\left(1-\frac{1}{k \pi}\right)} \geq \frac{1}{\left(\frac{1 \pi}{2 \pi}\right.} \sum \limits_{k=2}^{n} \frac{1}{\sqrt{k-1}} \xrightarrow{n \rightarrow \infty} \infty \\ \geqslant \sqrt{\left(\frac{1}{k \pi(k-\pi \pi \pi}-\frac{1}{(k-\pi \pi \pi}\right)^{2}} \\ =\sqrt{\left(\frac{1}{(k-\pi \pi \pi}\right)^{2}\left(\frac{1}{k \pi}-1\right)^{2}} \\ =\frac{\sqrt{1-\frac{1}{k \pi}}}{\sqrt{k-1} \pi / 2} \geqslant \frac{\sqrt{1-\frac{1}{k}}}{\sqrt{k-1} \pi^{1 / 2}} \geqslant \frac{1}{\sqrt{2}} \sqrt{\sqrt{k}-1 / 2 / 2}=\frac{1}{\sqrt{2 \pi}} \frac{1}{\sqrt{k-1}} \\ \end{array} \)
Also ich habe die Länge L(c) nach unten abgeschätzt bis zu dem letzten Ausdruck da unten. Da dieser Ausdruck dann für wachsende n, divergiert, tut es dann automatisch auch L(c). Hierbei musste ich diese Supremum- Definition nutzen und konnte nicht das mit der Integraldefinition für die Länge einer Kurve machen, da c nicht stetig-differenzierbar ist…
Habe ich das richtig gemacht?