Du kannst die Gleichung nach y auflösen:
$$ y = 0,5 · \sqrt [ 3 ] { x ^ { 2 } } \pm \sqrt { 0,25 · \sqrt [ 3 ] { x ^ { 4 } } + 1 - x ^ { 2 } } $$
Als zwei Graphen gezeichnet:
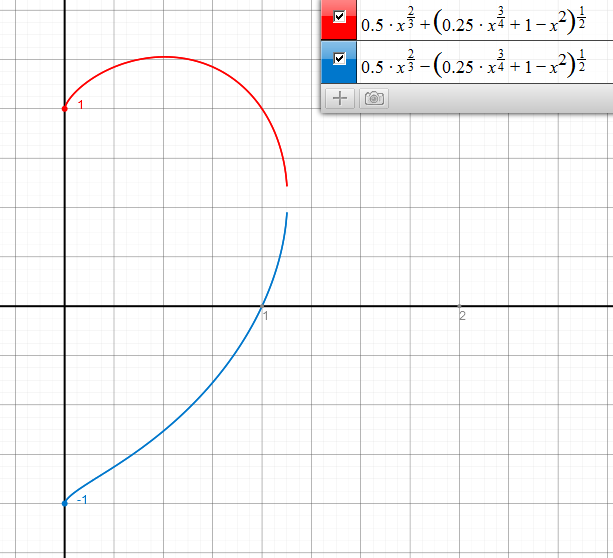
Der Plotter zeichnet hier nicht ganz zu Ende, aber beide berühren sich!
Den Punkt unten kannst du ermitteln, indem du für die Funktionsgleichung (blauer Graph) x = 0 setzt, dann erhältst du für y:
$$ \begin{array} { l } { y = 0,5 · \sqrt [ 3 ] { x ^ { 2 } } - \sqrt { 0,25 · \sqrt [ 3 ] { x ^ { 4 } } + 1 - x ^ { 2 } } } \\ { y = 0,5 · \sqrt [ 3 ] { 0 ^ { 2 } } - \sqrt { 0,25 · \sqrt [ 3 ] { 0 ^ { 4 } } + 1 - 0 ^ { 2 } } } \\ { y = - \sqrt { 0 + 1 } } \\ { y = - \sqrt { 1 } } \\ { y = - 1 } \end{array} $$
Den Punkt oben erhältst du über den Hochpunkt aus der Funktionsgleichung (roter Graph). y ≈ 1,237 (siehe Antwort Julian-Mi)
Den Punkt rechts erhältst du, indem du den Schnittpunkt der beiden Graphen berechnest (zur nummerischen Berechnung hat Julian-Mi bereits etwas geschrieben). Siehe nachstehend. Lösung x ≈ 1,139
$$ \begin{array} { l } { 0,5 · \sqrt [ 3 ] { x ^ { 2 } } - \sqrt { 0,25 · \sqrt [ 3 ] { x ^ { 4 } } + 1 - x^2 } = 0,5 · \sqrt [ 3 ] { x ^ { 2 } } + \sqrt { 0,25 · \sqrt [ 3 ] { x ^ { 4 } } + 1 - x ^ { 2 } } } \\ { - \sqrt { 0,25 · \sqrt [ 3 ] { x ^ { 4 } } + 1 - x ^ { 2 } } = \sqrt { 0,25 · \sqrt [ 3 ] { x ^ { 4 } } + 1 - x ^ { 2 } } } \end{array} \\ \begin{array} { l } { - \left( 0,25 · \sqrt [ 3 ] { x ^ { 4 } } + 1 - x ^ { 2 } \right) = 0,25 · \sqrt [ 3 ] { x ^ { 4 } } + 1 - x ^ { 2 } } \\ { 0 = 0,25 · \sqrt [ 3 ] { x ^ { 4 } } + 0,25 · \sqrt [ 3 ] { x ^ { 4 } } + 1 + 1 - x ^ { 2 } - x ^ { 2 } } \\ { 0 = 0,5 · \sqrt [ 3 ] { x ^ { 4 } } - 2 x ^ { 2 } + 2 } \end{array} $$
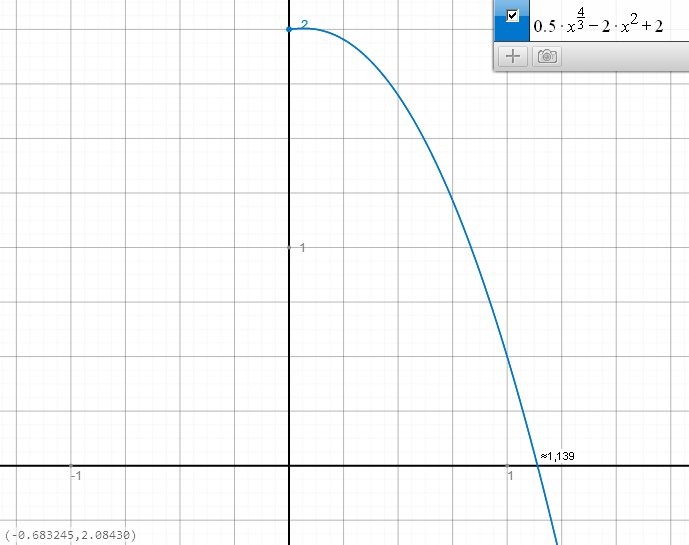
Der Graph dieser "Nullstellenfunktion" sieht wie folgt aus. Du siehst hier auch, dass die Funktion bei x ≈ 1,139 eine Nullstelle hat:
Zusammenfassung:
So hast du also für die Höhe -1 bis 1,237 und für die Breite -1,139 bis 1,139.
Demnach einen Umfang für das Rechteck von: 2*2,237 + 2*2,278 = 4,474 + 4,556 = 9,03