
Text erkannt:
Sufgabe 2. a
Un wissen:
\( b_{1} v_{1}+\ldots+b_{n} v_{n}=0 \quad \Rightarrow b_{1}=b_{2}=\ldots=b_{n}=0 \)
Var: Jede dK der vi, die den Nulluellur ergëff, hamn nuer die hiwiale sein
\( z_{2}: a_{1} v_{1}+a_{2}\left(v_{1}-v_{2}\right)+a_{3}\left(v_{1}-v_{3}\right)+\cdots+a_{n}\left(v_{1}-v_{n}\right)=0 \Rightarrow a_{4}=\ldots=a_{n}=0 \)
Bewris:
\( \begin{array}{l} a_{1} v_{1}+a_{2}\left(v_{1}-v_{2}\right)+a_{3}\left(v_{4}-v_{3}\right)+\ldots+a_{n}\left(v_{1}-v_{n}\right)=0 \\ \Leftrightarrow a_{n} v_{1}+a_{2} v_{1}-a_{2} v_{2}+a_{3} v_{1}-a_{3} v_{3}+\ldots+a_{n} v_{1}-a_{n} v_{n}=0 \\ \Leftrightarrow\left(a_{1}+\ldots a_{n}\right) v_{1}-a_{2} v_{2}-a_{3} v_{3}-\ldots-a_{n} v_{n}=0 \\ \Longleftrightarrow b_{1} v_{1}+b_{2} v_{2}+\ldots+b_{n} v_{n}=0 \end{array} \)
\( b \) Dabie ist:
\( \begin{array}{l} b_{1}=\left(a_{1}+a_{2}+\ldots+a_{n}\right) \\ b_{i}=-a_{i} \text { fin } i=2, \ldots, n \\ b_{1} v_{1}+b_{2} v_{2}+\ldots+b_{n} v_{n}=0 \Rightarrow b_{1}=\ldots b_{n}=0 \\ \Leftrightarrow\left(a_{1}+a_{n}\right)=\ldots=-\left(a_{2}+\ldots+a_{n}\right)=9 \\ \end{array} \)
Ups habe ich übersehen, wieso ist denn die letzte Zeile falsch? Hier sind noch die restlichen Aufgaben, sind die richtig?
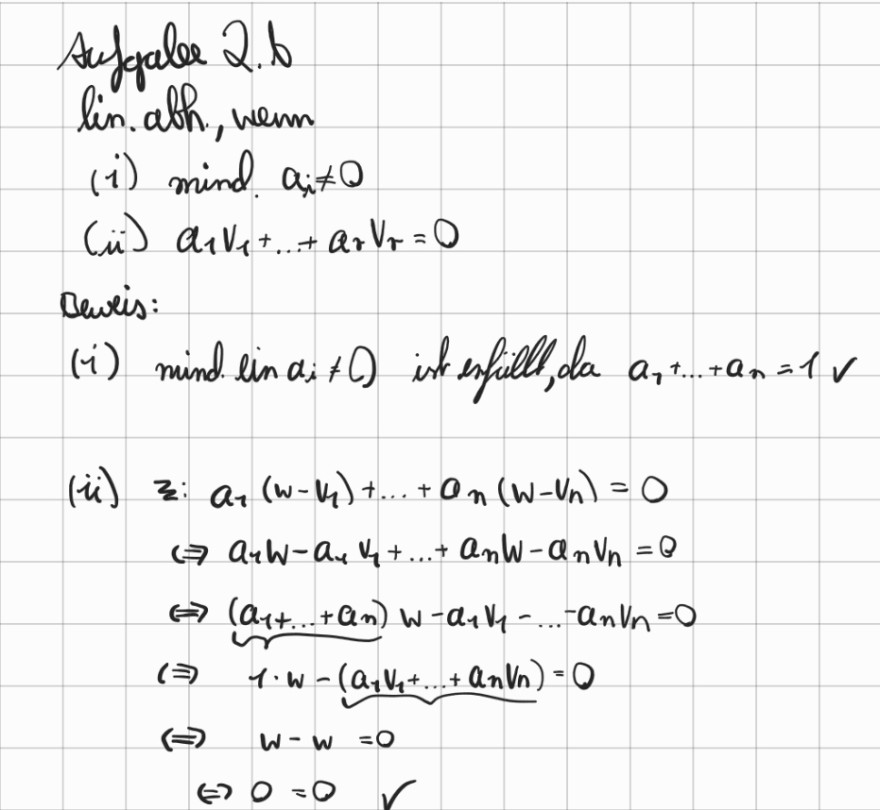
Text erkannt:
Aufgalee 2.6 lin. abh, wem
(i) mind \( a_{i} \neq 0 \)
(ii) \( a_{1} v_{1}+\ldots+a_{r} v_{r}=0 \)
Blwes:
(i) mind ein \( a_{i}+C \) ) ist erfiell, da \( a_{1}+\ldots+a_{n}=1 v \)
(ii)
\( \begin{array}{l} \text { z: } a_{1}\left(w-v_{1}\right)+\ldots+a_{n}\left(w-v_{n}\right)=0 \\ \Leftrightarrow a_{1} w-a_{1} v_{1}+\ldots+a_{n} w-a_{n} v_{n}=0 \\ \Leftrightarrow\left(a_{1}+\ldots+a_{n}\right) w-a_{1} v_{1}-\ldots-a_{n} v_{n}=0 \\ \Leftrightarrow 1 \cdot w-\left(a_{1} v_{1}+\ldots+a_{n} v_{n}\right)=0 \\ \Leftrightarrow w-w=0 \\ \Leftrightarrow 0=0 \quad \checkmark \end{array} \)

Text erkannt:
Aufgabe 2.c
\( w-v_{1}, \ldots, w-v_{n} \) fillen Busis van \( V \) wem,
(i) Ereagendensystem van \( l \)
(ii) linear unathängy
Beweis:
(i) Jeder Vellor \( v \in V \) laish scich als dimeanhonb schinilen: \( w=a_{1} v_{1}+\ldots+a_{n} v_{n} \in V \) und \( w-v_{1}, \ldots, w-v_{n} \quad \checkmark \)
(ii) Wi wisen:
Kar:
\( \begin{array}{l} a_{1} v_{1}+\ldots+a_{n} v_{n}=0 \Rightarrow a_{1}=\ldots=a_{n}=0 \\ \xi_{1} a_{1}\left(w-v_{1}\right)+\ldots+a_{n}\left(w-v_{n}\right)=0 \Rightarrow a_{1}=\ldots=a_{n}=0 \\ \Leftrightarrow a_{n} w-a_{n} v_{1}+\ldots+a_{n} w-a_{n} v_{n}=0 \\ \Leftrightarrow\left(a_{n}+\ldots+a_{n}\right) w-a_{n} v_{1}-\ldots-a_{n} v_{n}=0 \\ \Leftrightarrow\left(a_{1}+\ldots+a_{n}\right) w-\underbrace{\left(v_{1}+\ldots+a_{n} v_{n}\right.}_{V_{n}: \Rightarrow a_{n}=\ldots})=0 \\ \Rightarrow 0 \cdot w-0=0 \end{array} \)
Nur bei Aufgb 2.c bei (i) weiß ich nicht wie konkret sagen kann: Ja deswegen ist das ein Erzeugendensystem, weil irgendwie ist es doch immer ein Erzeugendensystem. Ansonsten habe ich die Aufgaben jetzt wesentlich besser verstanden.