Hallo Joachim,
schneide einen großen Kreis von 40,1cm Durchmesser aus. Der Winkel, den Du raus schneiden musst, beträgt 91° (lass aber die Klebefläche stehen) und der kleine Kreis hat einen Durchmesser von 10cm.
Die Rechnung:
Gegeben sind die Höhe \(h\) des Kegelstumpfs, der große Durchmesser \(D\) und der kleine (obere) \(d\).
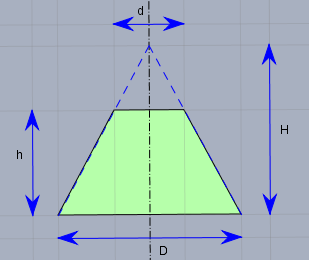
Dann berechnet man zunächst die Höhe \(H\) des fiktiven Kegels nach dem Strahlensatz$$\frac{H}{D} = \frac{H-h}{d} \implies H = \frac{Dh}{D-d}$$Und daraus die Seitenlänge \(S\) von der Spitze zum Boden und die Seitenlänge \(s\) von der Spitze zum oberen Kreis$$S=\sqrt{H^2 + \left(\frac{D}{2}\right)^2} \\ s = \sqrt{\left(H-h\right)^2+\left(\frac{d}{2}\right)^2} \space \text{oder}\, s = S\cdot \frac{d}{D}$$\(S\) ist gleichzeitig der Radius des großen Kreises, den Du ausschneiden musst, und \(s\) der Radius des inneren Kreises.
Der benötigte Winkel \(\alpha\) aus der Kreisscheibe ist$$ \alpha = \frac{D}{2S} \cdot 360°$$bzw. der, den man ausschneiden muss ist der Rest vom Vollkreis$$\beta = 360° - \alpha$$
Gruß Werner