Zuerst die Formeln für den Kegelstumpf herausgekramt:
V = h * Π / 3 * (R² + R*r + r²)
O = Π * r² + Π*R² + Π*m*(r + R)
r ist Kegelradius, R ist Radius des weggeschnittenen Kegels, m ist die Mantellinie (Außenkante)
bekannt: r = 7 cm, R = 4 cm
gesucht: m (Mantellinie)
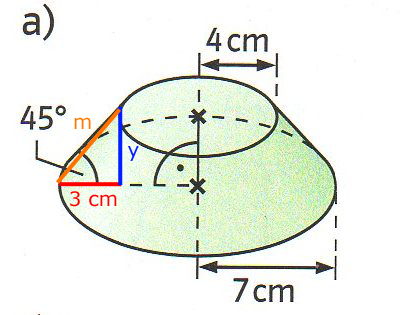
Lösung mit Hilfe der Trigonometrie:
cos (45°) = AK / HY
cos (45°) = 3 cm / m
1 / cos (45°) = m / 3 cm
3 cm * 1 / cos (45°) = m
m ≈ 4,2426 cm
Eingesetzt in:
O = Π * r² + Π*R² + Π*m*(r + R)
O = Π * (7 cm)² + Π*(4 cm)² + Π*(4,2426 cm)*(7 cm + 4 cm)
O = Π * 49 cm² + Π*16 cm² + Π*(4,2426 cm)*(11 cm)
O = Π * 49 cm² + Π*16 cm² + Π*(4,2426 cm)*(11 cm)
O = 350,817 cm²
Für das Volumen fehlt noch die Höhe h bei V = h * Π / 3 * (R² + R*r + r²)
Die Höhe h entspricht unserem y, also Sinus oder Tangens verwenden!
tan(45°) = GK/AK
tan(45°) = y/3 cm
tan(45°) * 3 cm = y
y = 3 cm = h
h in V:
V = h * Π / 3 * (R² + R*r + r²)
V = 3 cm * Π / 3 * ((4 cm)² + (4 cm)*(7 cm) + (7 cm)²)
V = Π cm * (16 cm² + 28 cm² + 49 cm²)
V = Π cm * (93 cm²)
V ≈ 292,168 cm³