- |2-x| und davon auf die - |2x|, was hat man genau für Zwischenschritte angewendet?

Question

Aufgabe:

Thema: Fourier Reihen,

für gerade Funktionen gilt ja f(x) = f(-x)

In einer Aufgabe lautet f(x) = - |2x| und es ist eine gerade Funktion.

Problem/Ansatz:

Es ist eine gerade Funktion, da f(x) = f(-x)

also: f(-x) = - |2-x| und das ist f(-x) = - |2x|, meine Frage ist wie man genau darauf kommt, erstmal wie kommt man auf die

 - |2-x| und davon auf die - |2x|, was hat man genau für Zwischenschritte angewendet?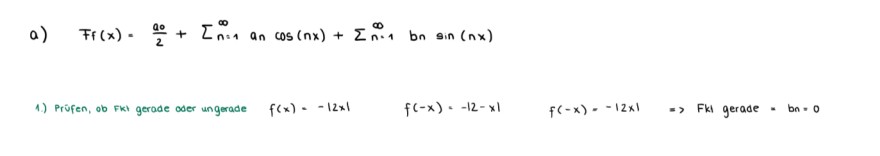

Text erkannt:

a) \( \quad F_{f}(x)=\frac{a_{0}}{2}+\sum \limits_{n=1}^{\infty} a_{n} \cos (n x)+\sum \limits_{n=1}^{\infty} \) bn \( \sin (n x) \)
1.) Prüfen, ob Fkt gerade oser ungerade \( f(x)=-|2 x| \quad f(-x)=-|2-x| \quad f(-x)=-|2 x| \quad \Rightarrow \) Fki gerade \( =b_{n}=0 \)

Answer 1

Hallo

das ist nur schlampige Schreibweise , richtig steht da |2*(-x)|=|-2*x| und Betrag sagt ja |-a|=|a|

Gruß lul

Answer 2

So etwas passiert eben, wenn man Klammern weglässt und nicht geschriebene Multiplikationszeichen ignoriert:

$$f(-x) = -\underbrace{|2(-x)|}_{{\color{red}\neq |2-x|}} = -|-2x| = -|2x|$$