Aufgabe:
3. Aufgabe „Extremwertbestimmung"
Gegeben ist eine rechteckige Scheibe, aus der ein dreieckiges Stück am unteren rechten Rand herausgebrochen ist (rot dargestellt). Welc he \( x-y \)-Koordinaten müssen Sie für den Punkt \( P \) wählen, damit die verbleibende rechteckige Scheibe (blau dargestellt) einen maximalen Flächeninhalt besitzt?
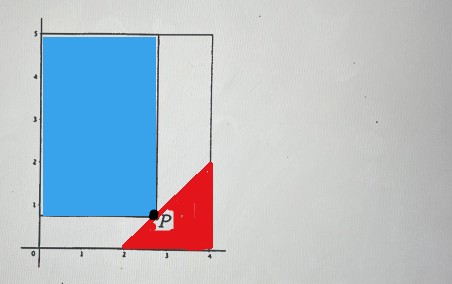
Tipp: Stellen Sie den Flächeninhalt des blauen Rechtecks als Funktion der \( x \)-Koordinate des Punktes \( P \) dar und vergessen Sie nicht die Randwerte zu untersuchen.
4. Aufgabe „Analytische Geometrie"
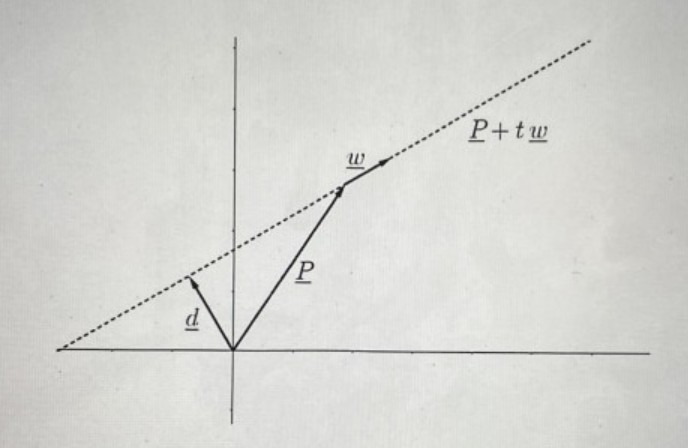
Gegeben ist eine Gerade \( g \) in Parameterdarstellung \( g=\{\underline{P}+t \underline{w} \mid t \in \mathbb{R}\} \). Hierbei wird \( \underline{w} \neq \underline{0} \) vorausgesetzt.
a) Bestimmen Sie den Vektor \( \underline{d} \), der vom Ursprung aus abgetragen auf einen Punkt der Geraden zeigt sowie senkrecht auf dieser steht. Orientieren Sie sich hierbei an der beigefügten Skizze. Bestimmen Sie anschließend mit Hilfe von \( \underline{d} \) die Normalform der Geraden, also eine Darstellung der Form \( g=\left\{(x, y) \in \mathbb{R}^{2} \mid a x+b y+c=0\right\} \).
b) Bestimmen Sie des Weiteren die Normalform konkret für den Fall \( \underline{P}=\left(\begin{array}{ll}2 & 4\end{array}\right)^{T} \) sowie \( \underline{w}=\left(\begin{array}{ll}1 & 1\end{array}\right)^{T} \). Bestimmen Sie auch den Abstand der Geraden vom Ursprung.
Tipp: Nutzen Sie die Eigenschaft (Skalarprodukt), dass \( \underline{d} \) senkrecht auf der Geraden steht und gleichzeitig auf einen Punkt der Geraden zeigt um den zugehörigen Wert von \( t \) zu berechnen.
Problem/Ansatz:
Hey kann mir jemand helfen die Aufgaben zu verstehen und im Bestfall eine Musterlösung präsentieren, danke. Mfg