Aufgabe:
In der Studie „Grenzen des Wachstums" wurden Prognosen über die mögliche Entwicklung der Chromvorräte auf der Welt veröffentlicht.
Szenario 1: Ab dem Jahr 1970 wird kein Chrom mehr verbraucht.
Szenario 2: Die Nutzungsrate bleibt ab dem Jahr 1970 konstant.
Szenario 3: Die Nutzungsrate nimmt jährlich um 2,6 % zu.
Szenario 4: Wie Szenario 3, aber mit dem fünffachen Chromvorrat.
Problem/Ansatz:
Wann sind die Chromvorräte jeweils erschöpft?
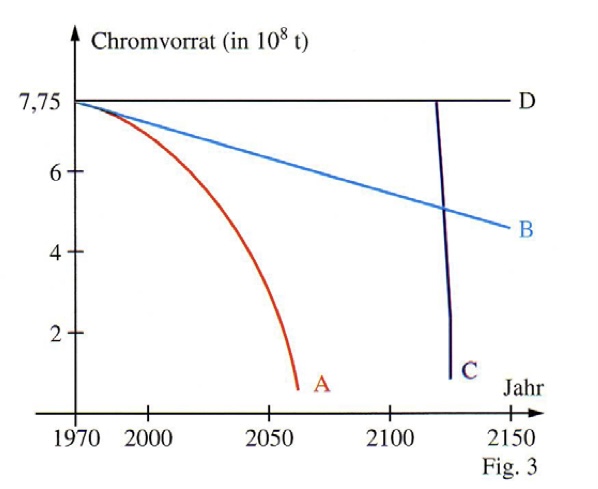
Hier werden die Nullstellen der jeweiligen Funktionen gesucht. Bei Funktion D wird die Nullstelle nie erreicht. Bei den Funktionen C und A kann man die Nullstellen noch einigermaßen abschätzen. Doch wie verhält es sich bei Funktion D? Da es sich um eine lineare Funktion handelt, wie berechne ich dort am besten die Nullstelle? Könnte man die Nullstellen auch bei C und A berechnen?
Gruß
Text erkannt:
Fig. 3