Bestimmen Sie einen Punkt D, sodass das Viereck ABCD ein Parallelogramm ist FRAGE

Question

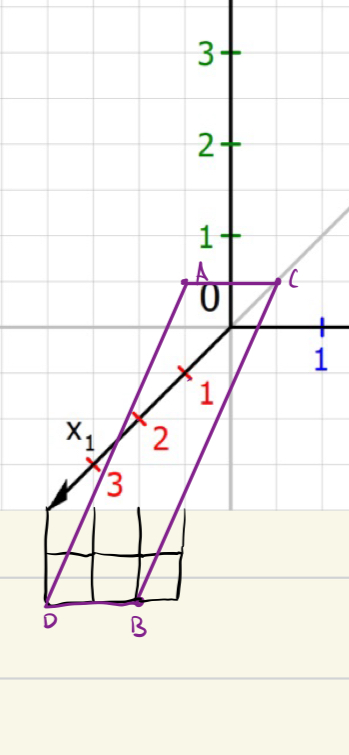
Gegeben ist das Dreieck ABC. Bestimmen Sie einen Punkt D, sodass das Viereck ABCD ein Parallelogramm ist.
a) A(3|1l2), B(2l0l-2), C(1|1l1)

Ich habe es eingezeichnet (siehe Foto).

Mein Ansatz war -> DA = -> BC

-> BC = (-1 / 1 / 3)

Und nun habe ich

(3 / 1 / 2) - (x / y / z) = (-1 / 1 / 3) gesetzt.

Dafür kam dann x = 4, y = 0, z = -1 raus und somit der Punkt D (4 l 0 l -1)

Allerdings ist die Lösung falsch. Es soll nämlich der Punkt D (2 l 2 l 5) rauskommen.

Allerdings verstehe ich meinen Fehler nicht.

Comments

Du hast versucht, das Drei- und Viereck zu skizzieren. Die Absicht war gut, die Umsetzung in einem dreidimensionalen Koordinatensystem ist aber nicht gelungen. Es war auch nicht nötig. Das Parallelogramm liegt in derselben Ebene wie das Dreieck. Man kann sich vorstellen, senkrecht auf diese Ebene zu schauen, und völlig ignorieren, wie die nun in einem dreidimensionalen Koordinatensystem genau liegt. Man muss das Dreieck auch nicht massstabsgetreu skizzieren. Es reicht, in irgendeinem skizzierten Dreieck die Ecken in der richtigen Reihenfolge anzuschreiben und sich dann zu überlegen, wo D etwa liegen soll, damit ein in der richtigen Reihenfolge angeschriebenes Parallelogramm entsteht. Und dann kommt man auf eine Vektorgleichung für D, beispielsweise so wie in meiner Antwort weiter unten. Dieses Vorgehen ist deutlich einfacher.

---

Dein Punkt D ist auch richtig. Achte auf die Aufgabenstellung:

Bestimmen Sie einen Punkt D, sodass das Viereck ABCD ein Parallelogramm ist.

Insgesamt gibt es 3 mögliche Punkte - deiner ist mit dabei:

---

Dein Punkt D ist auch richtig. Achte auf die Aufgabenstellung:

Das sehe ich nicht so, wenn man sich an die Konvention der Benennung ebener Figuren hält, siehe dazu auch den Kommentar zu meiner Antwort. Ein Viereck \(ABCD\) ist eben nicht dasselbe Viereck wie das Viereck \(ADBC\). Und nur weil in der Aufgabe ein unbestimmter Artikel steht, heißt das nicht, dass es mehrere Lösungen geben muss.

Answer 1

\( \displaystyle \overrightarrow{OD} = \overrightarrow{OA} +\overrightarrow{BC} = \begin{pmatrix} 2\\2\\5 \end{pmatrix}\)

Dabei habe ich die Konvention der Eckpunktbenamsung bei Drei- und Vierecken befolgt, nämlich in alphabetischer Reihenfolge im Gegenuhrzeigersinn.

Answer 2

Dein Fehler ist, dass du dich nicht an die Konvention bei der Benennung von ebenen Figuren hältst. Die Eckpunkte werden immer alphabetisch gegen den Uhrzeigersinn beschriftet. Wenn du deine Zeichnung entsprechend anpasst, siehst du, dass nicht \(\overrightarrow{DA}=\overrightarrow{BC}\) gelten muss, sondern \(\overrightarrow{AD}=\overrightarrow{BC}\).

Dein Ansatz ist aber vollkommen richtig und wenn du den Fehler ausbesserst, solltest du auch auf das richtige Ergebnis kommen.

Comments

Ahh ich verstehe es! Aber wieso nimmt am. AD und BC und nicht zum Beispiel AC und BD?

---

Das sind doch die Diagonalen. Die sind doch nicht gleich! Mach eine korrekte Skizze mit richtiger Beschriftung (das reicht auch zweidimensional) und dann siehst du, warum das nicht passen kann.

---

Nimmt man immer AD und BC? Sind das immer die Diagonalen bei einem Parallelogramm?

---

Wenn du mal endlich eine Skizze machen würdest, dann könntest du dir die Frage selbst beantworten.

Wenn das Viereck \(ABCD\) heißt, dann sind die Ecken gegen den Uhrzeigersinn entsprechend beschriftet. Das von dir gezeichnete Viereck hätte die bspw. die Bezeichnung \(ADBC\).

Answer 3

Man zeichne sich ein Parallelogramm und darin die Vektoren AD und BC. Du solltest sehen, dass diese gleich sind.

Ebenso sind die Vektoren AB und DC gleich. Die könntest du dir selber einzeichnen. Die Vektoren der Diagonalen AC und BD sind aber nicht gleich. Auch das solltest du erkennen können.

Comments

Gegeben ist das Dreieck ABC. Bestimmen Sie einen Punkt D, sodass das Viereck ABCD ein Parallelogramm ist.

a) A(3|1l2), B(2l0l-2), C(1|1l1)

AD = BC
D - A = BC
D = A + BC = [2, 2, 5]

Eingezeichnet in ein dreidimensionales Koordinatensystem sieht es dann wie folgt aus: