Aufgabe:
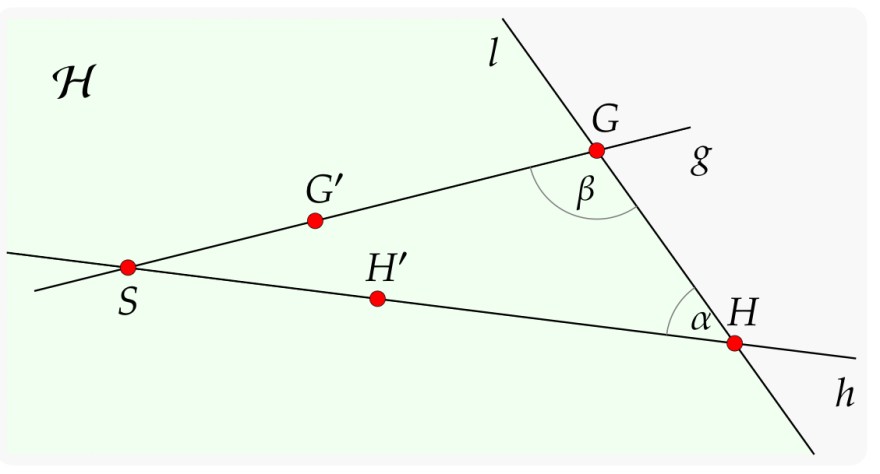
Seien \( g \), \( h \) und \( l \) drei Geraden, und sei \( g \cap l=\{G\} \) und \( h \cap l=\{H\}, G \neq H \). Seien \( G^{\prime} \in g \) bzw. \( H^{\prime} \in h \) zwei weitere Punkte auf \( g \) bzw. \( h \), die auf derselben Seite von \( l \) (also in derselben Halbebene in Bezug auf l) liegen.
Wenn|∢(G′GH)| + |∢(GHH′)| < 180◦,
dann schneiden einander die Geraden \( g \) und \( h \) in einem Punkt, der auf derselben Seite von 1 (also in derselben Halbebene in Bezug aufl) liegt wie die Punkte \( G^{\prime} \) und \( H^{\prime} \).
Zeigen Sie Wenn |∢(G′GH)| + |∢(GHH′)| = 180◦
gilt, dann sind die Geraden g und h parallel (schneiden einander also nicht). (Anschaulich ist das wohl klar: Die Aufgabe besteht darin, die Aussage logisch auf das Parallelenaxiom zurückzuführen.)
Hinweis: Versuchen Sie einen indirekten Beweis und betrachten Sie auch die andere Halbebene in bezug auf die Gerade l (aus dem Parallelenaxiom)
Problem/Ansatz:
Ich weiß nicht wie ich bei solchen Aufgaben vorgehe, oben das Parallelenaxiom auf das ich die Aussage zurückführen soll, ich verstehe aber nicht wie ich das logisch schlussfolgern kann