Question

Ist meine Matrix richtig?

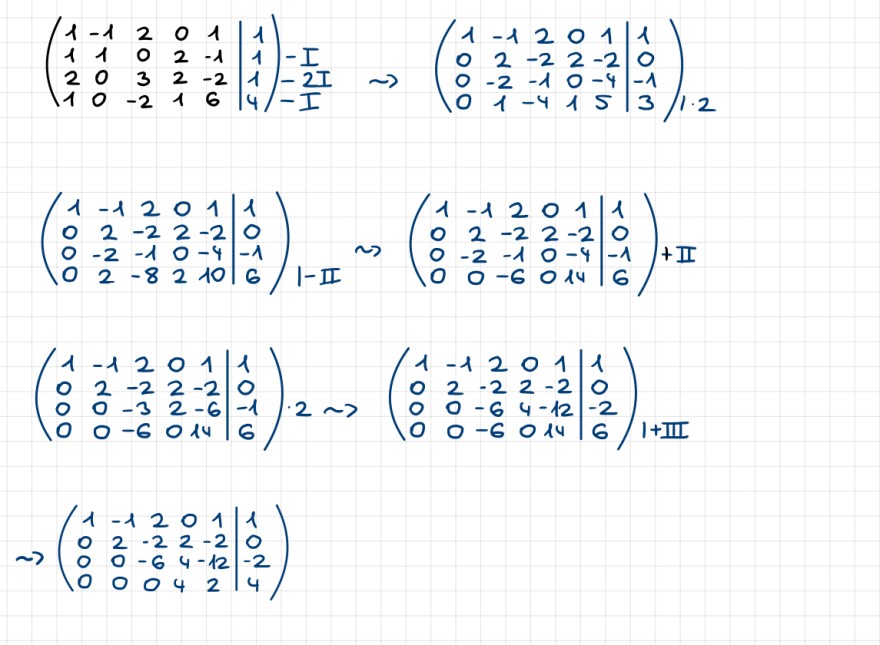
Text erkannt:

\( \begin{array}{l} \left(\begin{array}{ccccc|c} 1 & -1 & 2 & 0 & 1 & 1 \\ 1 & 1 & 0 & 2 & -1 & 1 \\ 2 & 0 & 3 & 2 & -2 & 1 \\ 1 & 0 & -2 & 1 & 6 & 4 \end{array}\right)-I \quad-I I \sim\left(\begin{array}{ccccc|c} 1 & -1 & 2 & 0 & 1 & 1 \\ 0 & 2 & -2 & 2 & -2 & 0 \\ 0 & -2 & -1 & 0 & -4 & -1 \\ 0 & 1 & -4 & 1 & 5 & 3 \end{array}\right)_{1 \cdot 2} \\ \left(\begin{array}{ccccc|c} 1 & -1 & 2 & 0 & 1 & 1 \\ 0 & 2 & -2 & 2 & -2 & 0 \\ 0 & -2 & -1 & 0 & -4 & -1 \\ 0 & 2 & -8 & 2 & 10 & 6 \end{array}\right) \text { |-III } \leadsto\left(\begin{array}{ccccc|c} 1 & -1 & 2 & 0 & 1 & 1 \\ 0 & 2 & -2 & 2 & -2 & 0 \\ 0 & -2 & -1 & 0 & -4 & -1 \\ 0 & 0 & -6 & 0 & 14 & 6 \end{array}\right)+\text { II } \\ \left(\begin{array}{ccccc|c} 1 & -1 & 2 & 0 & 1 & 1 \\ 0 & 2 & -2 & 2 & -2 & 0 \\ 0 & 0 & -3 & 2 & -6 & -1 \\ 0 & 0 & -6 & 0 & 14 & 6 \end{array}\right) \cdot 2 \sim\left(\begin{array}{ccccc|c} 1 & -1 & 2 & 0 & 1 & 1 \\ 0 & 2 & -2 & 2 & -2 & 0 \\ 0 & 0 & -6 & 4 & -12 & -2 \\ 0 & 0 & -6 & 0 & 14 & 6 \end{array}\right) 1+\text { III } \\ \sim\left(\begin{array}{ccccc|c} 1 & -1 & 2 & 0 & 1 & 1 \\ 0 & 2 & -2 & 2 & -2 & 0 \\ 0 & 0 & -6 & 4 & -12 & -2 \\ 0 & 0 & 0 & 4 & 2 & 4 \end{array}\right) \end{array} \)

Answer 1

Das sieht gut aus. In der zweiten Matrix, dritte Zeile, zweite Spalte muss +2 stehen.

Comments

Der matrizenrechner zeigt, dass die letzte Zeile eine Nullzeile sein muss, woran erkenne ich wie ich die Dreiecksform bzw. Die Nullform machen soll, bei 3x3 Matrizen war das ja noch einfach aber hier komme ich nicht so klar

---

Ah, sehe gerade. Eintrag \((3,2)\) in der zweiten Matrix muss +2 sein. Da war doch ein kleiner Vorzeichenfehler versteckt. ;)