Flächenbeziehung der Integration und Umkehrfunktion und Differentiation und Umkehrfunktion, einer Funktion f(x)=x^3-2x

Question

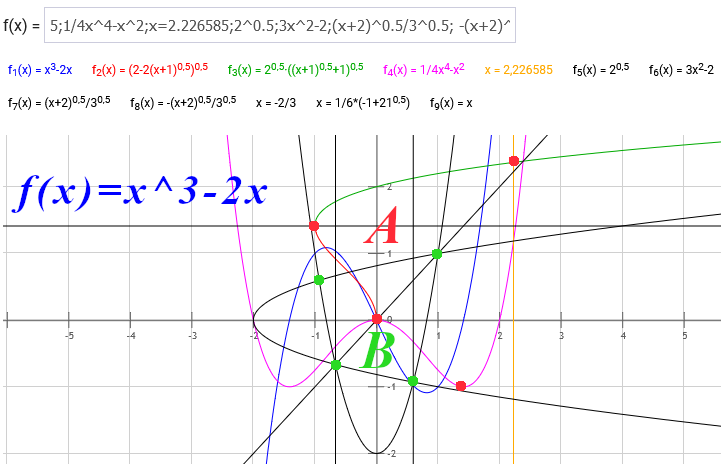
Aufgabe:

Verhältnis der eingeschlossenen Fläche, der von den Graphen der Differentiation und Ihrer Umkehrfunktion, sowie der Graphen der Integration und Ihrer Umkehrfunktion mit modifizierter Integrationsgrenze, einer Funktion f(x)=x^3-2x

Problem/Ansatz:

auf diese Berechnungen aufbauend, siehe Link: https://www.mathelounge.de/1095319/integration-umkehrfunktion-differentiation-umkehrfunktion

f(x)=x^3-2x f'(x)=3x^2-2            Umkehrfunktion: f'_u=+- (x+2)^0.5/(3)^0.5    F(x)=1/4x^4-x^2      Umkehrfunktion: F_u1=+-(2-2*(x+1)^0.5)^0.5  und F_u2=+-2^0.5*((x+1)^0.5+1)^0.5
Berechnung der von der Ableitungsfunktion und ihrer Umkehrfunktion eingeschlossenen Fläche: Schnittpunkte:
3x^2-2=(x+2)^0.5/3^0.5    a=1, b=-1/6*(1+(21)^0.5), c=1/6*(-1+(21)^0.5), d=-2/3

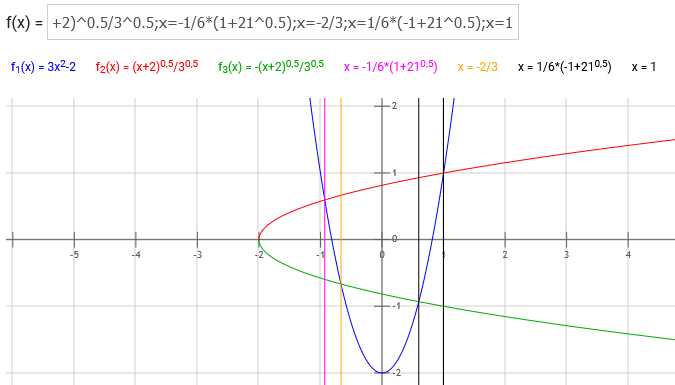
Berechnung der eingeschlossenen Fläche:

Integral von -(3b^2-2) bis (3a^2-2)  (x+2)^0.5/3^0.5 dx=2-0,425758=1,57422

Integral von -(3d^2-2) bis (3c^2-2)   (x+2)^0.5/3^0.5 dx=1,610943-0,59259=1,01835

1,57422+1,01835= 2,59257=B      ()^2=6,72142        B^2=A

Berechnung der von der Integrationsfunktion und ihrer Umkehrfunktion eingeschlossenen Fläche mit modifizierter Integrationsgrenze:

(x+2)^0.5/3^0.5=1/4x^4-x^2   dies ist die modifizierte Integrationsgrenze..... a=2,22658   b=-1

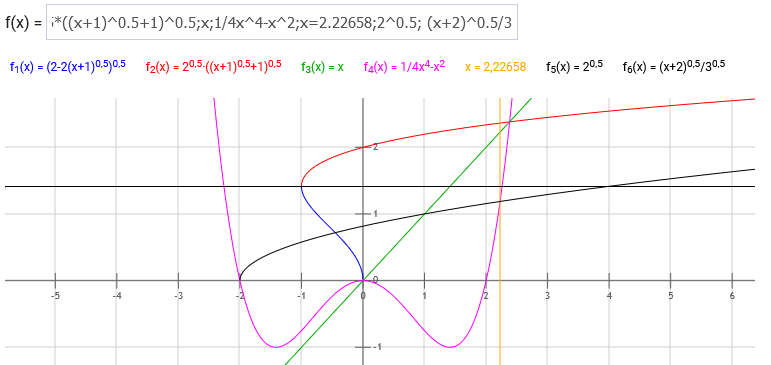
Integral von (2-2(b+1)^0.5)^0.5 bis (1/4a^4-a^2)  (2^0.5*((x+1)^0.5+1)^0.5) dx=5,975835+0,75425=6,73=A

Vergleiche: 6,73 ist fast genau 6,72142

den Fehlerwert würde ich auf das Rechnen mit ungenauen Dezimalstellen festlegen

Die gesamte Rechnung ist jedoch von der modifizierten Integrationsgrenze abhängig, damit steht und fällt alles.

Ich erbitte deshalb Ihre Meinungen dazu, auch im Hinblick auf die ganz oben im Link angezeigten "Vorbetrachtungen".

Comments

Habe das jetzt nicht nachgerechnet, aber deine Integrationsgrenzen sind seltsam. Du hast doch - auch in deiner Zeichnung - die senkrechten Geraden eingezeichnet. Warum nimmst du nicht diese Werte auch als Grenzen? Warum schreibst du bspw. Terme der Form \(-(3b^2-2)\), obwohl eigentlich genau \(b\) deine Grenze ist?

---

Die Grenzen werden doch durch eine Funktion festgelegt.....!

---

Nö, durch die Schnittstelle.

---

Vielleicht hilft es Bert besser zu verstehen, wenn man sich alte Beiträge durchliest.

https://www.mathelounge.de/user/Bert/questions

---

.....das ist nicht sachlich von Euch....., die jeweilige Endfassung meiner Arbeiten ist unter folgenden Link zu finden......

http://www.wichmann.dashosting.de/

....wisst Ihr, ich spiele manchmal Schach, amateurhaft, nur zum Spaß......

---

Ich verstehe jetzt das Problem nicht. Du wolltest doch Anmerkungen haben. Wenn du sie nicht willst, solltest du deine Rechnungen halt nicht veröffentlichen. Mein Kommentar war ja rein fachlicher Natur. Ich weiß also nicht, was daran nun unsachlich sein soll. Davon abgesehen hast du bspw. meine Antwort und Anmerkung zu deiner anderen Frage auch gekonnt ignoriert.

---

ein Beispiel, daß meine Integrale korrekt berechnet wurden:

Integral von 0 bis 2 -(1/4x^4-x^2) dx=1,066667= Integral von

(2-2(b+1)^0.5)^0.5 bis (1/4a^4-a^2) (2^0.5*((x+1)^0.5+1)^0.5) dx mit a=beliebig, größer 0 und b=-1, x=0   siehe www.Integralrechner.de

dies ergibt sich durch die Spiegelung der Funktionen an der Achse y=x, es wurden ja die Umkehrfunktionen ermittelt

Answer 1

Ich kann deine Ergebnisse nicht bestätigen.

Für das Integral zwischen den Graphen der Ableitung und seiner Umkehrfunktion erhalte ich ca. \(2.62962962963\) und für das Integral zwischen den Graphen der Integralfunktion und seiner Umkehrfunktion erhalte ich ca. \(7.01565159188\).

Ein quadratischer Zusammenhang zwischen diesen Werten liegt nicht vor, denn

\(2.62962962963^2=6.91495198901\).

Dein Beispiel und deine Notation sind dermaßen unübersichtlich und aus meiner Sicht auch überhaupt nicht schlüssig.

Integral von 0 bis 2 -(1/4x4-x2) dx=1,066667= Integral von

(2-2(b+1)0.5)0.5 bis (1/4a4-a2) (20.5*((x+1)0.5+1)0.5) dx mit a=beliebig, größer 0 und b=-1, x=0

Du hast eine variable obere Grenze, die von \(a>0\) beliebig abhängt. Für \(x=0\) ist dein Integrand konstant (also eine Zahl). Wie soll da für jedes beliebige \(a\) dann immer der Wert 1,066667 herauskommen? Vielleicht meinst du das Richtige, aber wie gesagt, deine Notation ergibt so überhaupt keinen Sinn.

Comments

darf ich noch fragen, wie Sie die Fläche zwischen dem Graphen der Ableitung und deren Umkehrfunktion berechnet haben........?

....ich habe dies nähmlich mit zwei unterschiedlichen Integralen, Lösungsansätzen, erzielt, dieses Ergebnis....

---

In deiner Notation:

\(I_{1}=\int_{-0.93043}^{-\frac{2}{3}}\!\big(f_2(x)-f_1(x)\big)\mathrm{d}x\)

\(I_{2}=\int_{-\frac{2}{3}}^{1}\!\big(f_2(x)-x\big)\mathrm{d}x\)

Und aus Symmetriegründen dann

\(A=2\cdot (I_1+I_2)\).