Aufgabe:
Es soll das Verhältnis der eingeschlossenen Fläche, der von den Graphen der Differentiation und Ihrer Umkehrfunktion, sowie der Graphen der Integration und Ihrer Umkehrfunktion, einer beliebigen Funktion aufgezeigt werden.
Problem/Ansatz:
ein einfaches Beispiel:
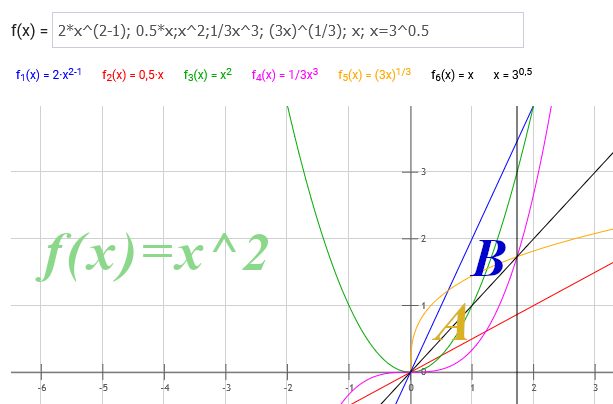
Funktion: f(x)=x^2
Differentiation f'(x)=(x^2)'=2x Umkehrfunktion fu=1/2x
Integration F(x)=1/3*x^3 Umkehrfunktion Fu=(3x)^(1/3)
Schnittpunkte von F(x) und Fu(x) ergibt: 1/3*x^3=(3x)^(1/3)
xs1=0 und xs2=3^(1/2)
Berechnung der eingeschlossenen Fläche der Graphen der Integration und Ihrer Umkehrfunktion:
Integral von 0 bis 3^(1/2) ((3x)^(1/3)-(1/3*x^3)) dx=1,5=A , siehe Bild
Berechnung der eingeschlossenen Fläche der Graphen der Differentiation und Ihrer Umkehrfunktion in den Grenzen der Integration:
Integral von 0 bis 3^(1/2) (2x-1/2x) dx=2,25=B, siehe Bild
A^2=B, diese Aussage ist Allgemeingültig bei einer derartige Konstellation der Gleichungen, mit den entsprechend modifizierten Integrationsgrenzen, was später an einem anderen, komplizierteren Beispiel, nicht heute, noch gezeigt wird.
Ich weiß, dies ist ein arg einfaches Beispiel, der Anschauung wegen gewählt.....! Da ist doch alles in Ordnung, oder?