Aufgabe:
Gegeben ist folgende Gleichung:
0,3 x ([(1.500-100x)÷50]÷x)⁰,⁷ = 0,7 × (x÷[(1.500-100x)÷50])⁰,³
Die korrekte Darstellung habe ich beigefügt. Es handelt sich um ein Foto aus einer von mir erstellen Word-Datei.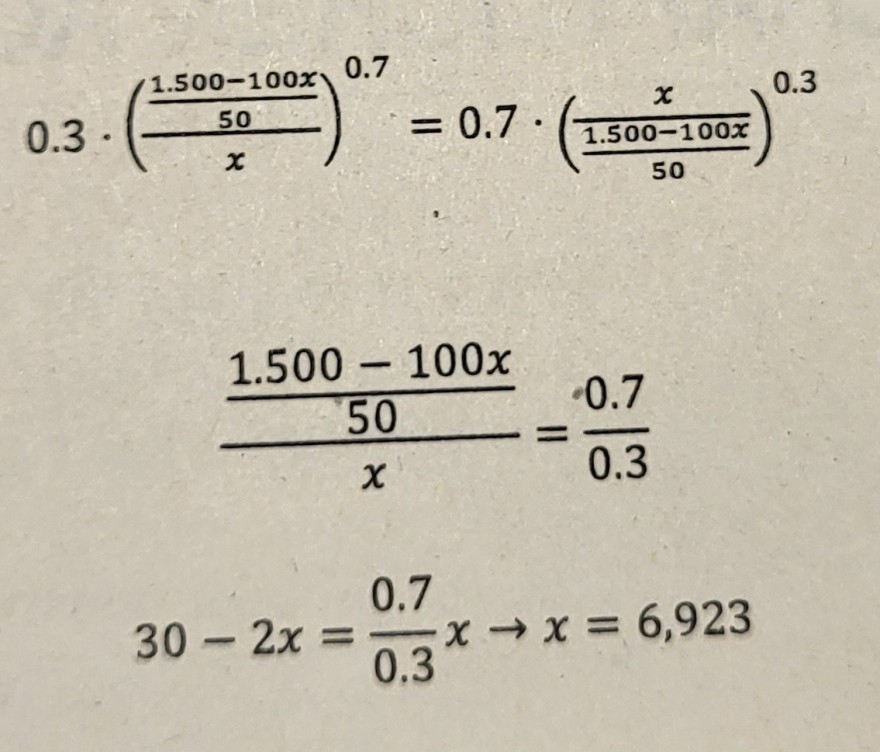
Text erkannt:
\( 0.3 \cdot\left(\frac{1.500-100 x}{50}\right)^{0.7}=0.7 \cdot\left(\frac{x}{\frac{1.500-100 x}{50}}\right)^{0.3} \)
\( \frac{\frac{1.500-100 x}{50}}{x}=\frac{0.7}{0.3} \)
\( 30-2 x=\frac{0.7}{0.3} x \rightarrow x=6,923 \)
Die Lösung lautet wie folgt:
1. Zwischenschritt: ([(1.500-100x)÷50]÷x) = 0,7÷0,3
2. Zwischenschritt: 30 - 2x = (0,7÷0,3)×x
Lösung: x = 6,923
Problem/Ansatz:
Ich verstehe nicht, wie man aus der Ausgangsgleichung auf den 1. Zwischenschritt kommt. Ich habe alle Regeln bei Potenzrechnung gesichtet und komme einfach nicht darauf, wie die Umstellung erfolgt. Über eine Erläuterung, gerne auch nur einen Hinweis auf die angewandte Regel, freue ich mich sehr.