Mustererkennung und Beweis

Question

Gegeben ist eine n×n-Matrix in deren k-ter Zeile die arithmetische Folge mit der konstanten Differenz k und dem Startglied k steht.

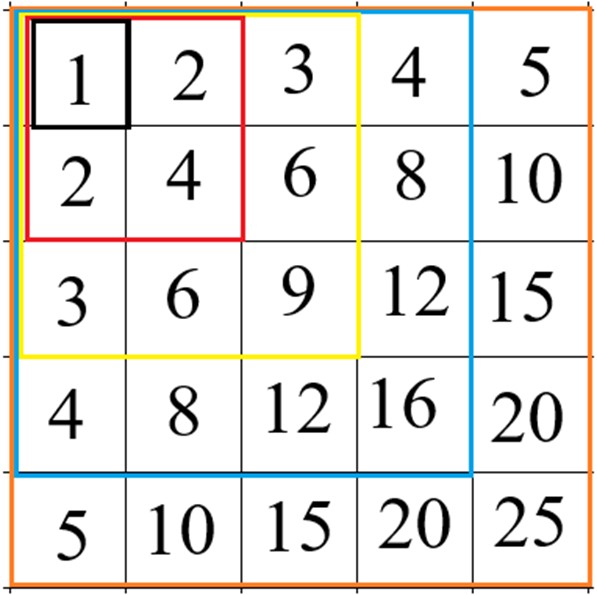
Teile in der linken oberen Ecke dieser Matrix quadratische Teilmatrizen der Ordnungen 1, 2, 3, 4, 5 usw. ab (hier: schwarz, rot, gelb, blau, orange) und berechne jeweils die Summe der Zahlen in einer solchen Teilmatrix. Beschreibe das Muster der gewonnenen Zahlenfolge formal in der Sprache der Mathematik, wenn die Ordnungen der Teilquadrate den natürlichen Zahlen zugeordnet sind, und beweise die Gültigkeit des beschreibenden Terms.

Comments

Diese Diskussion könnte noch ein interessantes Beispiel für Godwins Gesetz werden...

Answer 1

Die Summe der ersten Zeile ist n(n+1)/2.

Die Summe der zweiten Zeile ist 2·n(n+1)/2.

Die Summe der dritten Zeile ist 3·n(n+1)/2.

...

Die Summe der n-ten Zeile ist n·n(n+1)/2.

Die Summe aller n Zeilen ist (1+2+3+...+n)·n(n+1)/2 =(n(n+1)/2)².

Answer 2

Zur \(n\)-ten Teilmatrix kommt die Summe \(2n\sum_{i=1}^{n-1}i+n^2=n^2(n-1)+n^2=n^3\) hinzu.

Eine Formel lautet also für die Summe der \(n\)-ten Teilmatrix \(\sum_{i=1}^n i^3\).

Comments

Quatsch. Es geht hier um die Matrix n = 5

---

Rede keinen Unsinn und lies gefälligst richtig.

---

Quatsch. Es geht hier um die Matrix n = 5

Mit deiner Lesekompetenz ist es wirklich nicht weit her.

Btw: Hast du inzwischen herausbekommen, warum nicht bei jeder Extremstelle die zweite Ableitung von 0 verschieden ist?

---

Gebe ein Gegenbeispiel wo dies falsifiziert wird

---

Gebe ein Gegenbeispiel wo dies falsifiziert wird

Ein Gegenbeispiel hat dir döschwo vor 21 Stunden geschrieben.

Na ja, mangelnde Lesekompetenz ...

---

Ich glaube DU kannst nicht eine notwendige Bedingung (Äquivalenz) mit einer hinreichenden Bedingung (Implikation) unterscheiden. Ich rede die ganze Zeit von einer hinreichenden Bedinigung und da ist meine Aussage korrekt.

Dad Gegenbeispiel von döschwo ist nur eine Falsifizierung, dass dies eine Äquivalenz ist, mehr nicht. Daher wach auf Mensch!

---

notwendige Bedingung (Äquivalenz) mit einer hinreichenden Bedingung (Implikation) unterscheiden.

Autsch... Komm, lass einfach gut sein.

---

Also ich kann lesen.

Du hattest einen Versuch unternommen, den Begriff "Extrempunkte" zu erklären:

Extrempunkte

Das sind die Nullstellen des Differentials der jeweiligen Funktion, welche bei dem Differenzial zweiten Grades keine Nullstellen sind.

Worüber wir noch gar nicht gesprochen haben: Du kannst ja nicht mal klar zwischen "Extrempunkt" und "Extremstelle" unterscheiden.

Hast du dich nicht langsam genug blamiert?

---

Ihr wollt mir (einen Doktor) Mathematik beibringen? Das ich nicht lache… Nochmal unterscheidet den Begriff einer Äquivalenz und einer Implikation!

---

Wie schön du immer den anderen Beiträgen ausweichst.

1. Deine oben zitierte "Definition" für Extrempunkte ist in zweierlei Hinsicht falsch, da sich anhand der Formulierung gar nicht ergibt, dass du hier nur eine hinreichende Bedingung nennst. Das erwähntest du erst jetzt in dieser Diskussion. Als Doktor der Mathematik sollte man die Problematik solcher Aussagen erkennen können.

2. Deine weiter oben gegebene Anmerkung, eine notwendige Bedingung sei eine Äquivalenz, ist ebenfalls falsch.

Die Existenz eines Doktortitels - jedenfalls im Fach Mathematik - darf daher zu Recht bezweifelt werden.

---

Ich gehe jetzt.

---

Apfelmännchen, auch deine Antwort verdient das Prädikat "Beste". Kombiniert mit abakus Beweis ergibt sich eine Variante des Beweises des Satzes. Das Quadrat der Summe der ersten n natürlichen Zahlen ist gleich der Summe der ersten n Kubikzahlen.