Ich beschäftige mich zur Zeit mit Ungleichungen und dem dazugehörigen Vorzeichendiagramm. Dazu habe ich ein paar Fragen:
1.) Wie erkenne ich bei einer Aufgabe, ob ein Vorzeichendiagramm sinnvoll ist oder nicht? Gegeben sei die Ungleichung 3x-5 > x - 3. Hier erkenne ich ja flott, dass ich die Ungleichung einfach lösen kann.
Woher weiß ich aber bei (x-1)(3-x) > 0 auf den ersten Blick, dass hier ein Vorzeichendiagramm sinnvoll ist? Ich soll alle Werte von x bestimmen, welche die Ungleichung erfüllen.
2.) Folgende Ungleichung mit dem Vorzeichendiagramm ist gegeben:
Für welche Werte von \( x \) gilt \( (x-1)(3-x)>0 ? \)
$$ \begin{array}{ll} {x-1>0} & {\text { wenn } x>1} \\ {3-x>0} & {\text { wenn } x<3} \end{array} $$
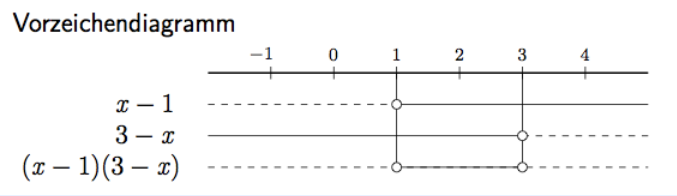
Woher erkenne ich, in welchem Intervall ich mich bewege wenn ich das Diagramm erstelle? Also woher weiß ich, dass beim Vorzeichendiagramm die Zahlen -1, 0, 1, 2, 3 und 4 ausreichend sind? Klar kann man rumprobieren aber gibt es einen Trick um das sofort zu sehen?
3.) (4x+1)/(x+3) < 0
Wie müssten die Faktoren bei dieser Ungleichung im Vorzeichendiagramm stehen?
(4x+1)
(x+3)
(4x+1)/(x+3)
War meine Idee. Ist das so richtig?
Danke