Quadratische Funktionen; Stromleitung

Question

Im Frühjahr wird eine Baustelle eingerichtet. Dazu wird über die Straße eine Stromleitung von Mast zu Mast gespannt. Die Masten stehen 20m voneinander entfernt. Die Stromleitung hängt parabelförmig nach unten durch.

Für die folgenden Berechnungen wurde ein Koordinatenkreuz eingezeichnet. Die x-Achse verläuft auf der Höhe der Straße. Die y-Achse geht durch die Straßenmitte. Eine Längeneinheit soll einem Meter entsprechen.

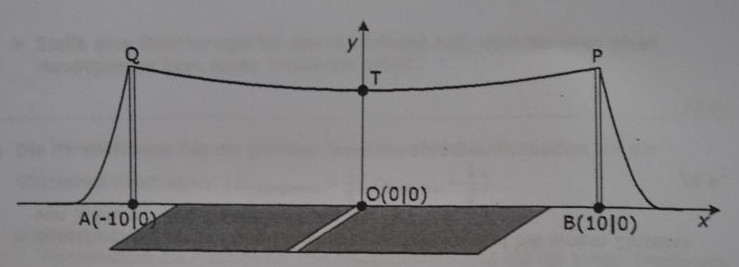
a) Die Parabel y=0,01x²+5 beschreibt die Form der durchhängenden Stromleitung.

→ Der tiefste Punkt der Stromleitung muss mehr als 4m über der Fahrbahn hängen, damit für durchfahrende Fahrzeuge ausreichend Platz bleibt. Bestimme die Höhe des tiefsten Punktes der Parabel über der Fahrbahn.
Entscheide, ob der Sicherheitsabstand eingehalten wird.

→ Der rechte Mast steht genau 10m von der Straßenmitte entfernt. Berechne, in welcher Höhe die Stromleitung über den Mast geführt wird.

Answer 1

a) Tiefste Punkt ist bei x = 0 -> y (x= 0) = 5 m

b) x= 10 oder x = -10 in die Funktion einsetzen -> y (x=10) = 0,01*10*10 + 5 = 6 m

Comments

Deine Antwort auf a) verstehe ich nicht.
Könntest du das bitte ausführlicher erklären ?

---

Wenn man das Koordinatensystem in den Punkt O (0|0) legt und sich vorstellt, dass die Symmetrieachse der nach oben geöffneten Parabel im Punkt 0 liegt, dann berechnet sich der tiefste Punkt der Parabel dadurch, dass man in die Funktion der Parabel für x den Wert Null einsetzt:

f(x =0) = 0,01*0² + 5 m = 5 m

Würde man einen Wert verschieden von 0 einsetzen, würde im Vergleich zu x = 0  für f(x) immer was größeres rauskommen.