Stromleitung quadratische Funktion

Question

Folgende Aufgabe lässt die Zeit bei mir verstreichen ohne auf ein Ergebnis zu kommen.

Bitte HILFE:

Stromleitungen sind in regelmäßigen Abständen an Strommasten im zum Teil unebenen Gelände fixiert. Die Spitzen zweier gleich hoher Strommasten liegen o,6km voneinander entfernt. Der rechte Mast steht aber um 40 Meter höher als der linke. In 200 m Entfernung hängt die Leitung um 20 m tiefer als an der linken Mastspitze. Die Form der Stromleitung kann näherungsweise durch eine Parabel beschrieben werden.

a) Stellen Sie eine Funktionsgleichung für diesen Sachverhalt auf.

b) Ermitteln Sie den teifsten Durchhangpunkt der Stromleitung und dokumentieren Sie Ihren Lösungsweg.

WIE MACHE ICH DAS?

Ich benötige bitte genaue Schritte.

Answer 1

Bedingungen

f(0)=0
f(200) = -20
f(600) = 40

Gleichungen

c = 0
40000a + 200b + c = -20
360000a + 600b + c = 40

Man erhält die Funktion

f(x) = 1/2400·x² - 11/60·x

Skizze

Comments

Nun kannst du die Funktion auf den Scheitelpunkt hin untersuchen.

---

Aber wie kann ich die Funktion auf den Scheitelpunkt untersuchen?

---

f(x) = ax^2 + bx + c

Die x-Koordinate des Scheitelpunktes ist immer

Sx = -b / (2a) = ...

Die y-Koordinate bekommst du immer durch einsetzen der x-Koordinate in die Funktion

Sy = f(Sx) = ...

Probierst du mal ob du das hin bekommst? Du kannst ja den Scheitelpunkt in etwa ablesen.

---

Liegen denn in diesem Fall die Spitzen der Strommasten tatsächlich 600m voneinander entfernt?

---

Nein. Nur die horizontale Entfernung von Mast zu Mast sind 600m. Will man die Entfernung von Spitze zu Spitze berechnen, dann kann man den Pythagoras nehmen.

---

Lt. Aufgabenstellung ist diese Entfernung gemeint. Sollte also nicht besser \(f\big(\sqrt{358400}\big)=40\) gelten?

---

Die Spitzen zweier gleich hoher Strommasten liegen o,6km voneinander entfernt. 

Wenn die Masten gleichhoch sind dann sind sie 600 m voneinander entfernt.

Da sie in Gleichen abständen stehen sind sie horizontal auch 600 m entfernt wenn einer höher ist.

---

Deiner Lösung zufolge liegen die Spitzen der Strommasten nicht 600m, sondern rund 601,33m voneinander entfernt.

---

Ah. Ich verstehe das Problem.

x^2 + 40^2 = 600^2 --> x = 160·√14 = 598.67

Bedingungen

f(0)=0 
f(200) = -20 
f(598.67) = 40

Gleichungen

c = 0
40000·a + 200·b + c = -20
3584057689/10000·a + 59867/100·b + c = 40

Man erhält die Funktion

f(x) = 332890/795572563·x² - 1461352563/7955725630·x
f(x) = 0.0004184282056·x^2 - 0.1836856411·x

---

Offensichtlich ist besagte Entfernung größer als sie sein sollte.

---

Du hast es anders Interpretiert.

 Die Spitzen zweier gleich hoher Strommasten liegen o,6km voneinander entfernt.

Ich hatte es interpretiert, wenn die Masten gleich hoch ragen sind sie 600 m entfernt. Diese Entfernung ist fest. Aber nun ragen die Spitzen halt unterschiedlich hoch ins Gelände.

Ich würde auch mein Standpunkt weiter so vertreten. Ich kann aber deine Argumentation verstehen. 

---

Inwiefern ist dann aber diese Interpretation mit deiner Zeichnung vereinbar?

---

x² + 40² = 600² --> x = 160·√14 = 598.67

wie kommt man auf √14 ???

---

x² + 40² = 600²

x² + 1600 = 360000

x² = 358400

x = ± √358400 = ± √(2^11·5^2·7) = ± √(2^10·5^2·2·7) = ± 2^5·5·√(2·7) = ± 160·√(14)

---

aha. und wie komme ich auf all diese klammerwerte? :)  ich versteh´s grad gar nicht.

---

Das ist eine Einfache Faktorzerlegung. Das lernt man in der 6. Klasse.

Du schreibst also 358400 einfach als malaufgabe. und zerteilts dabei die Faktoren immer weiter bis alle Faktoren Primzahlen sind. Das nennt sich dann auch Primfaktorzerlegung.

---

 Danke. Jetzt fühl ich mich besser. Ja, ich weiß, ich bin ein Matheidiot.

---

Meist langt ja auch wenn du das einfach als Dezimalzahl hinschreibst. Zumindest für viele Lehrer. Ich habe oben ja auch mit dem Dezimalwert dann weitergerechnet. Die Aufgabe ist auch wenn man sie nach der Alternative rechnet nicht so schön. Scheint wohl aber so gemeint zu sein.

---

Ich danke dir! Lieben Gruß!

Answer 2

war nix, der Versuch

Comments

Skizze: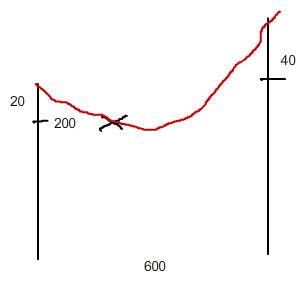

Punkte  (0;0) Spitze linker Mast

      (200;-20 )  und  (600;40)

in Y = ax^2 +bx +c einsetzen

c=0    und    40000*a +200b=-20   und  360000a+600b=40

                                  b= -0,1 - 200a   und  360000a -60 - 120000a = 40

                                                                         240000 a =  100

                                                                                    a = 1/2400

                               b = -1/10 -200/12000 = -1/10 - 1/60 = -11/60

gibt y= 1/2400x^2 - 11/60 x

Nullstellen bei 0 und 440 also Scheitel bei 220

mit y-Wert  -121/6 ungefähr -20,17

Also hängt es am tiefsten Punkt 20,17m gegenüber der linken Mastspitze durch.