Extrempunkte berechnen (Notwendige Bedingung/Hinreichende Bedingung)

Question

Wie geht man bei der folgenden Funktion vor?             f(x)=x^3+3x^2-9x

Comments

Weis einer vielleicht wie man noch die Wendepunkte berechnet?

---

Notwendige Bedingung: f''(x) = 0

Hinreichend: f''(x) = 0 und f'''(x) ≠ 0

Die zweite Ableitung war f''(x) = 6x+6

Die dritte ist also f'''(x) = 6

 

f''(x) = 6x+6 = 0

x = -1

 

Es ist f'''(-1) = 6 und damit haben wir an der Stelle x = -1 eine Wendestelle.

In f(x) eingesetzt:

W(-1|11)

Answer 1

Hi,

 

Erster Schritt: Ableitungen bilden

f(x) = x^3+3x^2-9x

f'(x) = 3x^2+6x-9

f''(x) = 6x+6

 

Not. Bedingung: f'(x) = 0

3x^2+6x-9 = 0     |:3, dann pq-Formel

x₁ = -3

x₂ = 1

 

Hinr. Bedingung: f'(x) = 0 und f''(x) ≠ 0

Wenn Du x_1,2 in f''(x) einsetzt, bekommst Du Werte ungleich 0.

f''(-3) < 0   -> Hochpunkt

f''(1) > 0   -> Tiefpunkt

 

Nun einsetzen in f(x)

H(-3|27)

T(1|-5)

 

Graphische Kontrolle:

 

Grüße

Answer 2

f(x)=x³+3x²-9x

f'(x)= 3x²+6x-9

f''(x)= 6x+6

 

1.Ableitung gleich Null setzen und nach x auflösen.

3x²+6x-9=0 |:3

x²+2x-3=0 |pq-Formel

x₁=1

x₂= -3

f''(x)= >0 T

f''(x)= <0 H

damit in die 2.Ableitung

f''(1)= 6*1+6= 12  TIefpunkt

f''(-3)= 6*(-3)+6 = -12  Hochpunkt

T(1|-5)

H(-3|27)

Answer 3

 

f(x) = x³ + 3x² - 9x

f'(x) = 3x² + 6x - 9

f''(x) = 6x + 6

 

Notwendige Bedingung für einen Extrempunkt: f'(x) = 0

Hinreichende Bedinung für ein Maximum: f''(x) < 0

Hinreichende Bedingung für ein Minimum: f''(x) > 0

 

f'(x) = 3x² + 6x - 9 = 0 | :3

x² + 2x - 3 = 0 | pq-Formel

x_1,2 = -1 ± √(1 + 3)

x₁ = -1 + 2 = 1

x₂ = -1 - 2 = -3

Das war die notwendige Bedingung.

 

f''(1) = 6 + 6 = 12 > 0, also Minumum an der Stelle x = 1

f''(-3) = -18 + 6 = -12 < 0, also Maximum an der Stelle x = -3

Das war die hinreichende Bedinung.

 

Nun brauchen wir noch die Funktionswerte; wir setzen in f(x) ein:

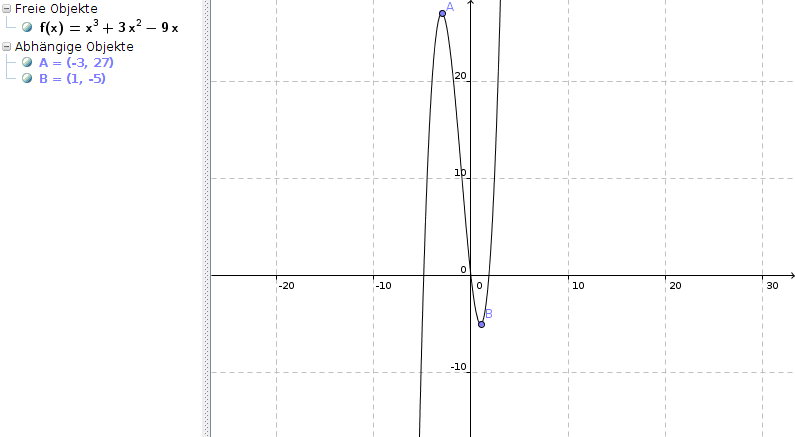
f(1) = 1 + 3 - 9 = -5 | Minimum an (1|-5)

f(-3) = -27 + 27 + 27 = 27 | Maximum an (-3|27)

 

 

Besten Gruß