Für eine endliche Gruppe (G,*) kann man eine Verknüpfungstafel aufstellen,
deren Einträge die Werte x * y für jedes Paar (x, y) ∈ G × G enthält. Betrachte folgende
unvollständige Verknüpfungstafel für eine Gruppe mit vier Elementen: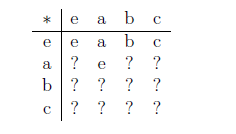
(hier sollen z.B. in der dritten Zeile die Verknüpfungen b * e, b * a, b * b, b * c angegeben
werden). Welche Möglichkeiten gibt es, um diese Tafel zu vervollständigen? Sind die
diesen Möglichkeiten entsprechenden Gruppen abelsch?
Hinweis: Zur Vereinfachung kann zur Lösung dieser Aufgabe darauf verzichtet werden, die
Assoziativität für alle möglichen Tripel von Elementen nachzuweisen. Man achte jedoch
darauf, ob die Assoziativität ausgenutzt werden kann, um die Tabelle zu vervollständigen.
So sieht es wohl richtig aus ;)