Kurvendiskussion von f(x) = 1/4*x^3-3/2*x^2+3*x - Kontrolle

Question

f(x)= 1/4x³-3/2x²+3x 

f'(x)= 0.75x²-3x+3 

f''(x)= 1.5x-3 

f''(x)= 1.5 

Symmetrie: 

Nein, es tauen gerade und ungerade Exponenten auf, also 2 und 3 und 1 und deshalb keine Symmetrie. 

Nullstellen:

1/4x³-3/2x²+3x |*4 

x³-6x²+12x 

x₁=0

ich denke es gibt keine weiteren Nullstellen oder? kann ich jetzt einfach die Nullstellen von -6x²+12x mit der pq-Formel berechnen? 

Extrema: 

1.Ableitung Null setzen und nach x auflösen: 

0.75x²-3x+3 = 0 |:0.75 

x²-4x+4=0 |pq-Formel 

x= 2 

f''(2)= 1.5x-3 = 0   also kein Extrema??? 

 

Und wie war nochmal grenzwert und so??? und Polstellen und Asymptoten die fehlen mir auch noch :( 

Answer 1

Hi Emre,

das ist soweit richtig.

Gibt kein Extrema, yup. Aber Wendepunkt kannst Du noch untersuchen ;).


Polstellen:

Haben wir keine, haben ja keine Definitionslücke bzw. eine Unbekannte im Nenner eines Bruchs.


Asymptote:

Wir haben ein Polynom. Gibt es keine.


Verhalten gegen unendlich:

Beachte die höchste Potenz. Positives Vorzeichen:

x->∞: f(x) = ∞

x->-∞: f(x) = -∞


Grüße

Comments

Ah den Wendepunkt habe ich ganz vergessen :) 

2.Ableitung gleich Null setzen und nach x auflösen: 

1.5x-3=0 |+3 

1.5x= 3 |:1.5 

x= 2 

f'''(2)= 1.5 ≠ 0  also ja ein Wendestelle 

Wendepunkt (2|2) :) hoffe das stimmt :) 

 

und die grenzwerte habe ich nicht verstanden...das war zu schnell....was ist mit der höhstenpotenz?? und warum steht dann da - unendlich??

---

Ja, das ist richtig. Das ist Dein Wendepunkt.

Wie Du festgestellt hattest, war ja f'(2) ebenfalls 0.

Das hat dann sogar einen speziellen Namen und wird Sattelpunkt (ab und an auch Terrassenpunkt) genannt.


Grenzwerte:

Du musst Dir überlegen was passiert, wenn Du (betragsmäßig) große Zahlen einsetzt. Da fällt Dir schnell auf, dass nur x^3 eine große Rolle spielt. Der Rest ist nicht so wichtig. Dann kommt man schnell auf das Verhalten. Sieht man auch gut im Graphen ;).

---

ja das weiß ich ja, aber kommt dann da auch eine negative zahl raus??? weil da steht ja miinnnuuuss:((((

sattelpunkt kenne ich nicht :) kann man das iweie auch berechnen?? oder ist das nur dann da, wenn es kein extrema gibt?

---

Setze x = -10.000

---

-2.5015003_{x|o¹¹ ??} 

---

Genau ;).

Das bedeutet Du hast also ein riiieeessiigge Zahl...negativ. Also ist die Annahme, dass f(x) gegen -∞ geht, nicht vom Himmel geholt.

Ansonsten schau auch bei Brucybabe im Graphen, wie das aussieht ;). Da geht es links ganz arg weit runter.

---

ahhhh hmm ok das kommt mir so vor, als hätte ich das jetzt v erstanden :)
und wenn man +10.000 für x einsetzt dann geht das gegen + unendlich?? oder??

---

So isses ;) .

Answer 2

Hi Emre :-)

 

ganz kurz: Alles richtig gemacht - sowohl die Ableitungen als auch die Schlussfolgerung zur (fehlenden) Symmetrie als auch die Schlussfolgerung, dass es keine Extrema gibt !!

 

Polstellen gibt es nicht, da Du für x jeden Wert einsetzen kannst.

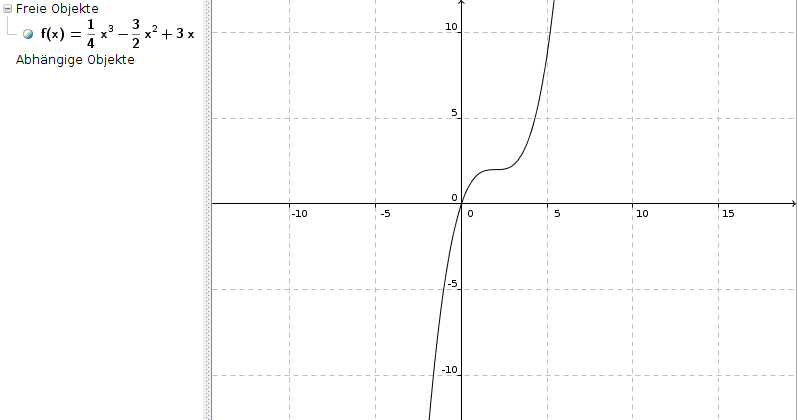
Wenn wir uns das Verhalten der Funktion im Unendlichen ansehen, stellen wir Folgendes fest:

x -> ∞ : Die Funktion wächst gegen ∞ (nur das 1/4 * x³ ist relevant, also der Term von x mit dem größten Exponenten),

x -> -∞: Die Funktion fällt gegen - ∞ (aus dem gleichen Grund wie eben geschrieben).

Die Funktion sieht so aus:

Lieben Gruß

Andreas

Comments

Hallo Andreas :)

ahh man ich bin immer so schnell :( (hab leider den Stern schon vergeben, aber Du und Unknown seit ja meine Favoriten) :D)
Danke auch natürlich an Dich!!!
Nächstes mal warte ich lieber:) (ich vergesse das immer^^)

---

Hallo Emre :-)

wichtig sind nicht die Sterne, sondern dass Du (bzw. ein/e andere/r Fragesteller/in) Nutzen aus den Antworten ziehst und Deine mathematischen Fähigkeiten erweiterst!

Und da das bei Dir ja in der Regel (eigentlich immer!) der Fall ist, sind die Sterne so unwichtig wie nur was :-D

Also mach Dir darüber bitte keine Gedanken!

Lieben Gruß

Andreas

---

Haha ja Du hast Recht.:)
Und  :)