Vielleicht hilft folgende (nicht maßstabsgerechte) Skizze weiter:
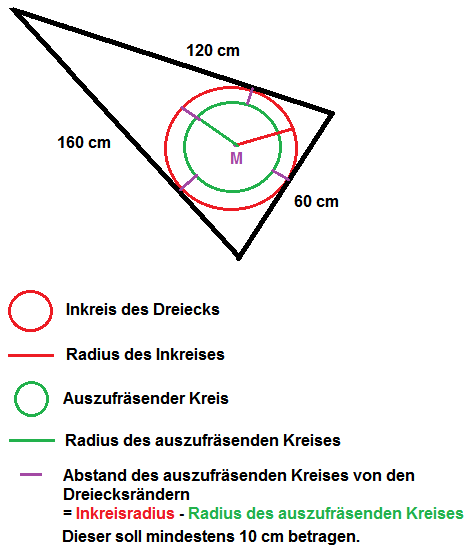
Zunächst: Wenn dies eine Aufgabe aus der 7.Klasse ist, dann vermute ich, dass der Schüler den gesuchten Radius nicht exakt berechnen soll, sondern dass er "lediglich" erkennen soll, dass der größte ausfräsbare Kreis denselben Mittelpunkt wie der Inkreis haben muss. Dann soll der Schüler eine entsprechende, maßstabsgetreue Skizze anfertigen (ähnlich meiner Skizze) und daraus den maximalen Radius des auszufräsenden Kreises abmessen.
Wenn allerdings eine exakte Berechung erforderlich ist, dann muss man zunächst den Radius des Inkreises aus den angegebenen Seitenlängen ermitteln. Subtrahiert man dann von diesem Radius 10 cm, so erhält man den unter den angegebenen Bedingungen maximalen Radius des auszfräsenden Kreises.
Für den Inkreisradius rinkreis gibt es folgende Formel:
rinkreis = 2 A / u
wobei A der Flächeninhalt und u der Umfang des Dreiecks ist.
Der Umfang u des Dreiecks ist leicht berechnet:
u = a + b + c = 140 + 60 + 120 = 320
Etwas schwieriger (weil aufwändiger) ist die Berechnung des Flächeninhaltes A des Dreiecks aus dessen Seitenlängen. Dafür gibt es mehrere Formeln, etwa die Heronsche Flächenformel, die Der_Mathecoach verwendet hat. Ich finde diese Formel etwas zu umständlich und bevorzuge folgende Formel:
16 A 2 = ( a 2 + b 2 + c 2 ) 2 - 2 ( a 4 + b 4 + c 4 )
(bei der allerdings recht große Zahlen als Zwischenergebnisse entstehen können. Dies kann man vermeiden, indem man z.B. in Metern statt in Zentimetern rechnet).
Durch Umformung ergibt sich daraus:
A 2 = ( ( a 2 + b 2 + c 2 ) 2 - 2 ( a 4 + b 4 + c 4 ) ) / 16
A = √ ( ( ( a 2 + b 2 + c 2 ) 2 - 2 ( a 4 + b 4 + c 4 ) ) / 16 )
Setzt man hier nun für a, b und c die angegebenen Werte ein, erhält man:
A = √ ( ( ( 140 2 + 60 2 + 120 2 ) 2 - 2 ( 140 4 + 60 4 + 120 4 ) ) / 16 )
= √ ( ( 1413760000 - 1208960000 ) / 16 )
= √ ( 204800000 / 16 )
= √ ( 12800000 )
und damit kann man nun den Inkreisradius nach der oben angegebenen Formel berechnen:
rinkreis = 2 A / u
= 2 * √ ( 12800000 ) / 320
= √ ( 12800000 ) / 160
= √ ( 12800000 / 160 2 )
= √ ( 500 )
= √ ( 100 * 5 )
= 10 * √ ( 5 )
≈ 22,36 cm (gerundet)
Der Radius rK des auszufräsenden Kreises darf also höchstens:
rK = 10 * √ ( 5 ) - 10 cm ≈ 12,36 cm
betragen.
Schlussbemerkung:
Angesichts dieser schönen "glatten" Zahlen, die sich hier ergeben,
z.B. A = √ ( 12800000 ) oder rInkreis = √ ( 500 ), könnte man auf die Idee kommen, dass meine eingangs geäußerte Vermutung doch nicht richtig ist, dass also der Schüler hier doch exakt rechnen soll ...