Wurzelgleichung √(x+6) - √(10-2x) = 1 Lösungen bestimmen

Question

Hallo hier die Aufgabe:

√(x+6) - √(10-2x) = 1

ich bringe zuerst √(10-2x) auf die andere Seite.

anschliessend quadriere ich um die Wurzel zu beseitigen. Hier ist auch mein Problem. Die Wurzel bei x+6 verschwindet, aber was mach ich auf der rechten Seite?

mfg

Comments

Auf der rechten Seite quadrierst du mit der binomischen Formel. Es bleibt ein Wurzel und noch sonst ein paar Terme.

Nun dafür sorgen, dass die Wurzel allein auf einer Seite steht und nochmals quadrieren. Inklusive binomische Formel auf der andern Seite.
Willst du das mal selbst versuchen?

Prinzip wie bei a) hier: https://www.mathelounge.de/37783/wurzelgleichung-√-x-1-√-2·x-5-3-und-ungleichung-x-2-x-3-x-x-2

---

Ja ich probiere erstmal selber
danke

Answer 1

 

√(x+6) - √(10-2x) = 1 | + √(10-2x), richtig

√(x+6) = 1 + √(10-2x) | Quadrieren, auch das ist richtig

x + 6 = 1 + 2*√(10-2x) + 10 - 2x | -1 - 10 + 2x

x + 6 - 1 - 10 + 2x = 2*√(10 - 2x)

 

3x - 5 = 2 * √(10 - 2x) | Trick: Nochmal quadrieren

9x² - 30x + 25 = 4 * (10 - 2x)

9x² - 30x + 25 = 40 - 8x | - 40 + 8x

9x² - 22x - 15 = 0 | :9

x² - 22/9 * x - 15/9 = 0

pq-Formel

x_1,2 = 11/9 ± √(121/81 + 135/81) = 11/9 ± √(256/81) = 11/9 ± 16/9

x₁ = 27/9 = 3

x₂ = -5/9

 

Unbedingt die Probe machen, da Quadrieren keine Äquivalenzumformung ist:

√9 - √4 = 3 - 2 = 1 | stimmt

√(6 - 5/9) - √(10 + 5/9) = √(49/9) - √(95/9) ≈ 7/3 - 9,75/9 ≠ 1

Die einzige Lösung ist also x = 3

 

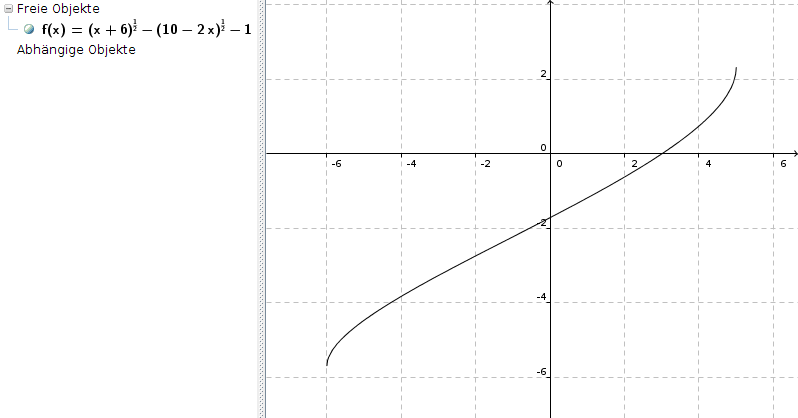
Zur grafischen Kontrolle habe ich

√(x+6) - √(10-2x) = 1

noch einmal umgeformt zu

√(x+6) - √(10-2x) -1 = 0

und dies so dargestellt:

Besten Gruß